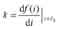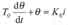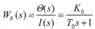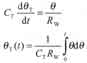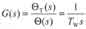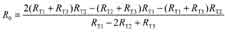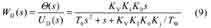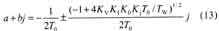一种EDFA温控电路的分析
时间:06-29
来源:互联网
点击:
1 引言
EDFA模块主要包括两部分:光路模块和电路模块。光路模块的功能是光信号的驱动放大,电路模块则用于对光路模块中泵源980nm激光器进行测控,使EDFA整机按预定预置的各项指标长期稳定、可靠的工作。本文设计了一种高精度、宽范围的温控电路。
2 980nmLD组件特性
2.1 980nmLD组件
980nmLD载体器件安装在半导体制冷器上,通过改变流过制冷器的电流方向(决定致冷或加热)和大小,调节载体的温度。载体上安装有热敏电阻 RT为温度传感器。
2.2 980nmLD的热传导模型
若流入(出)载体的热量速率为q , 载体向周围散发(吸收)的热量速率为qs ,根据热力学定律有如下关系:
Cdθ/dt=q-qs (1)
式中,C是载体的热容量。载体温度 θ的大小决定于i流过半导体制冷器产生的电功率。因而 q与i为函数关系,且为非线性关系:q = f (i)。 由于最关心的是稳定值(亦工作点Θ 0 ,I0)附近的变化。为此,将函数 q = f (i)进行线性化处理;并考虑到:
qs=θ/R (2)
R是载体向周围传热的热阻;并令: CR=T0,T0是 θ(t)变化的时间常数;kR=K 0,
则式(1)可写成动态方程:
这就是流过半导体制冷器的电流I (t)与载体温度q(t)的动态微分方程。若 i(t)象函数为I(s);q (t)的象函数为Q(s),则式(4)可写成传递函数形式:
显然,这是一个惯性环节。
设热敏电阻RT的热容量为 CT,载体向热敏电阻输出热量的速率为 qT,热阻为RW。在载体温度 θ的作用下,RT的温度θ T由以下方程描述:
用传递函数表示:θ(t) 象函数为Θ(s): θT(t)象函数为Θ T(s)则
其中,TW=C TRW,这是积分环节。
3 用于温度稳定的(模拟)自调系统
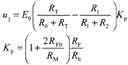
为了使980nmLD稳定在预置(或给定)的温度上,温控系统应设计成自调系统。该系统的调节对象是“制冷器”,输出量是载体温度 θ(t),象函数是Θ(s);输入量,亦给定值以电压形式 uD(t)输入,其象函数为U D(t),则自调节系统方框图如图1所示。以下给出组成方框图各部分的硬件电路,然后对系统的品质和误差进行分析和检测。
3.1 可控恒流源
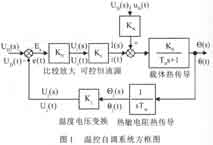
在图1温控系统中,可控恒流源实质上是执行机构。图2(a)是可控恒流源电原理图。图中:IC1是电流取样负反馈放大器;IC2是误差放大器,;T1 、T2构成电流放大器。
图2(a)是由电流负反馈电路构成的恒流源。输出恒流i(t)流入制冷器。经推导i (t)与输入(控制)电压ui( t)有如下关系:
显然KI为常数。这就是说,恒流源的输出与运放及晶体管参数无关,只与电阻R1、 R2和R0有关。因此,本恒流有很高的稳定性。图2(b)中,由T3~T6构成桥开关。由数字开关信号 Vp(TTL电平)控制恒流源输出电流的方向。
3.2 温度测量反馈电路
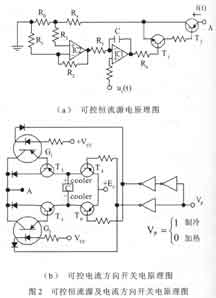
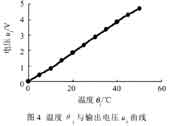
由于载体温度与热敏电阻R T的阻值为单值单调对应关系。因此,通过检测装在载体中的热敏电阻 RT的阻值来确定载体温度。图3是常用的温度-电压变换电桥电路。
由图可知,电桥输出(uT -u0),再经放大得:
若对应温度q1 、q2、q3的输出定为 u01、 u02 u03,则线性化的条件是u 02=(u03-u01 )/2。为简化,令u01=0,u 02= u03/2,根据R1和 q的对应关系,可选q1=0℃,q 2=25℃,q3=50℃,对应的电阻为: R T1,R T2和R T3,满足三点线性化的方程组:
解方程得:
将R T1、R T2、RT3代入上式得:R 0=7.837kΩ,并计算出θj- uj曲线,如图4所示,该曲线在0℃、25℃和50℃三点满足线性化条件,曲线近似成直线,则 Ui(t)=K jqj(t) (8)
Kj为直线斜率,计算得 Kj=94.387mV/℃。
3.3 系统品质分析
由图1,可得输入为给定量象函数U D(s),输出为温度象函数Θ(s ),温度自调节系统的传递函数:
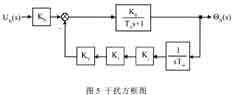
当给定值不变,或UD (s)=0,扰动电压UN(s ),温度变化ΘN(s),方框图如图5所示。
由图5可得在UN( s)作用下的扰动传递函数:
由图1,当UN(s )=0状态下,得出误差信号e(t)的象函数 E(s):
由式(9)~(11),对系统品质如下分析。 (1)无静差系统
若扰动信号uN( t)=1(t),扰动静差qN (t)可根据终值定理求得:
其中:UN(s )=1/s,引入式 (10),则:
为无扰动静差。由式 (11),不难求得给定静差。令UD(s )=1/s,则给定静差:
e(t)|=limsxE(s)=0
(2)最佳状态
由式(9)可写出系统的特征方程:
T0s2 +s+KVKI K0Kj/T W =0 (12)
首先判断系统是否稳定。由式(12)可知,方程的各阶系数均大于零,且不缺项,根据代数法稳定判据,系统稳定。
再根据方程的根:
因图1中的比较放大器KV 是比例放大器(电路图略),改变放大器的比例电阻,亦可改变 KV。改变KV可使系统出现三种状态:欠阻尼状态、过阻尼状态、临界状态,若使4KVK IK0KjT 0/TW 在0附近,则系统进入临界状态,此时上升时间短而又不振荡,为最佳状态。实验表明此时 KV为40~50。
EDFA模块主要包括两部分:光路模块和电路模块。光路模块的功能是光信号的驱动放大,电路模块则用于对光路模块中泵源980nm激光器进行测控,使EDFA整机按预定预置的各项指标长期稳定、可靠的工作。本文设计了一种高精度、宽范围的温控电路。
2 980nmLD组件特性
2.1 980nmLD组件
980nmLD载体器件安装在半导体制冷器上,通过改变流过制冷器的电流方向(决定致冷或加热)和大小,调节载体的温度。载体上安装有热敏电阻 RT为温度传感器。
2.2 980nmLD的热传导模型
若流入(出)载体的热量速率为q , 载体向周围散发(吸收)的热量速率为qs ,根据热力学定律有如下关系:
Cdθ/dt=q-qs (1)
式中,C是载体的热容量。载体温度 θ的大小决定于i流过半导体制冷器产生的电功率。因而 q与i为函数关系,且为非线性关系:q = f (i)。 由于最关心的是稳定值(亦工作点Θ 0 ,I0)附近的变化。为此,将函数 q = f (i)进行线性化处理;并考虑到:
qs=θ/R (2)
R是载体向周围传热的热阻;并令: CR=T0,T0是 θ(t)变化的时间常数;kR=K 0,
|
则式(1)可写成动态方程:
|
这就是流过半导体制冷器的电流I (t)与载体温度q(t)的动态微分方程。若 i(t)象函数为I(s);q (t)的象函数为Q(s),则式(4)可写成传递函数形式:
|
显然,这是一个惯性环节。
设热敏电阻RT的热容量为 CT,载体向热敏电阻输出热量的速率为 qT,热阻为RW。在载体温度 θ的作用下,RT的温度θ T由以下方程描述:
|
用传递函数表示:θ(t) 象函数为Θ(s): θT(t)象函数为Θ T(s)则
|
其中,TW=C TRW,这是积分环节。
3 用于温度稳定的(模拟)自调系统
为了使980nmLD稳定在预置(或给定)的温度上,温控系统应设计成自调系统。该系统的调节对象是“制冷器”,输出量是载体温度 θ(t),象函数是Θ(s);输入量,亦给定值以电压形式 uD(t)输入,其象函数为U D(t),则自调节系统方框图如图1所示。以下给出组成方框图各部分的硬件电路,然后对系统的品质和误差进行分析和检测。
|
3.1 可控恒流源
在图1温控系统中,可控恒流源实质上是执行机构。图2(a)是可控恒流源电原理图。图中:IC1是电流取样负反馈放大器;IC2是误差放大器,;T1 、T2构成电流放大器。
|
图2(a)是由电流负反馈电路构成的恒流源。输出恒流i(t)流入制冷器。经推导i (t)与输入(控制)电压ui( t)有如下关系:
显然KI为常数。这就是说,恒流源的输出与运放及晶体管参数无关,只与电阻R1、 R2和R0有关。因此,本恒流有很高的稳定性。图2(b)中,由T3~T6构成桥开关。由数字开关信号 Vp(TTL电平)控制恒流源输出电流的方向。
3.2 温度测量反馈电路
由于载体温度与热敏电阻R T的阻值为单值单调对应关系。因此,通过检测装在载体中的热敏电阻 RT的阻值来确定载体温度。图3是常用的温度-电压变换电桥电路。
|
由图可知,电桥输出(uT -u0),再经放大得:
|
若对应温度q1 、q2、q3的输出定为 u01、 u02 u03,则线性化的条件是u 02=(u03-u01 )/2。为简化,令u01=0,u 02= u03/2,根据R1和 q的对应关系,可选q1=0℃,q 2=25℃,q3=50℃,对应的电阻为: R T1,R T2和R T3,满足三点线性化的方程组:
|
解方程得:
|
将R T1、R T2、RT3代入上式得:R 0=7.837kΩ,并计算出θj- uj曲线,如图4所示,该曲线在0℃、25℃和50℃三点满足线性化条件,曲线近似成直线,则 Ui(t)=K jqj(t) (8)
Kj为直线斜率,计算得 Kj=94.387mV/℃。
|
3.3 系统品质分析
由图1,可得输入为给定量象函数U D(s),输出为温度象函数Θ(s ),温度自调节系统的传递函数:
|
当给定值不变,或UD (s)=0,扰动电压UN(s ),温度变化ΘN(s),方框图如图5所示。
|
由图5可得在UN( s)作用下的扰动传递函数:
由图1,当UN(s )=0状态下,得出误差信号e(t)的象函数 E(s):
由式(9)~(11),对系统品质如下分析。 (1)无静差系统
若扰动信号uN( t)=1(t),扰动静差qN (t)可根据终值定理求得:
其中:UN(s )=1/s,引入式 (10),则:
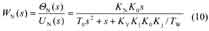 |
为无扰动静差。由式 (11),不难求得给定静差。令UD(s )=1/s,则给定静差:
e(t)|=limsxE(s)=0
(2)最佳状态
由式(9)可写出系统的特征方程:
T0s2 +s+KVKI K0Kj/T W =0 (12)
首先判断系统是否稳定。由式(12)可知,方程的各阶系数均大于零,且不缺项,根据代数法稳定判据,系统稳定。
再根据方程的根:
|
因图1中的比较放大器KV 是比例放大器(电路图略),改变放大器的比例电阻,亦可改变 KV。改变KV可使系统出现三种状态:欠阻尼状态、过阻尼状态、临界状态,若使4KVK IK0KjT 0/TW 在0附近,则系统进入临界状态,此时上升时间短而又不振荡,为最佳状态。实验表明此时 KV为40~50。
电路 半导体 电流 电阻 传感器 电压 放大器 电路图 单片机 显示器 相关文章:
- 一种新型防伪读码器的设计(01-01)
- 基于ARM与DSP的嵌入式运动控制器设计(04-25)
- 航天器DC/DC变换器的可靠性设计(02-12)
- 基于ARM核的AT75C220及其在指纹识别系统中的应用(05-24)
- 基于nRF2401智能小区无线抄表系统集中器设计(04-30)
- 卫星电源分系统可靠性设计与研究(02-12)