预测和负延迟滤波器：你应该知道的五件事

作者：赛普拉斯半导体 Kendall Castor-Perry

所有系统，包括滤波器，都是因果关系。这意味着它们不能在激励源激励之前对激励（不可预知）做出任何反应。那么，又该如何设计一款可“预测”的滤波器呢？好吧，这一切都取决于你对品质的期待有多高以及这一预测的相关性。

那么，我们再次祭起曾非常流行的“五件你应该知道的事”这一招式之旗，我们提出五个核心问题，其答案可以帮助我们绕过这个“滤波器”陷阱。

滤波器如何延缓信号？

信息可以通过多种方式加载于信号，它总是需要一段限定的时间来通过处理系统。你可能很熟悉数字模块的传输延迟概念。延迟，就是在输入发生某些状态变化到输出发生相应状态变化这段时间差。有数字概念的读者首先想到的可能是一个‘1’和‘0’的码流，以作为不同电压或电流水平的物理表述。对于这样的信号，传输延迟没有害处；但当我们考虑到模拟信号（实际上，没有确定的特性对应特定的时间点）时，就不是那么简单了。

我们经常对信号和数据序列进行低通滤波以消除“噪声”--高频率变异，我们已确定其没有任何意义，且它还是我们要观察的更重要的基本频点的障碍。虽然滤波过程对我们的观察影响巨大，但它绝对是一个影响观察的案例。当我们查看响应图形时，传统滤波方式最明显的后果是，在输入信号的变化和滤波后输出的相应变化之间有明确的时间延迟。当我们看一些例子时，我们将在某一时刻借助测试信号清楚地看到这点。

我们如何量化这种形式的延迟？

滤波器（或任何其它线性信号处理模块）输入信号和相应输出之间的这种“滞后”，

与组延迟紧密相关，组延迟相当于（或略低于）相位响应与派生频率。为此应选用明智的单位；如果你用弧度测量相位，以其每秒弧度的角形式表达频率，那么，（弧度）除以（弧度每秒），你就可得到以秒表示的答案。或者你可以使用“周期”—— 一个周期，是一个完整旋环，或360度。相位差以周期表示，除以赫兹（与每秒的周期数相同）表示的常规频率差，也会给出以秒表述的答案。

我们可能忍不住要问：如果要避免这种滞后，为什么不设计一款没有任何组延迟的滤波器？如果你以前读过我的专栏，你可能会认识到这句话中的“危险成分”。因为，你猜对了——它并非这么容易。如果你查找或计算“标准”的低通滤波器响应，你会发现，他们的组延时是总是正向的，一直降到零频率。这里，我们需要来点别出心裁。

我们可以消除（或者不仅仅是消除）这种延迟吗？

如果你想让延迟在任一频率都为零，那严格的答案是‘不能'。但确实有种技术可用以开发补偿滤波器，当其与原来的滤波器级联时，可以给你零延迟；当DC时，甚至是负的组延迟。正如我们将看到的，这可能非常有用。你不需要进行任何试错——现在，可将麻烦扼杀在未发。

比方说，某种低通传递函数H，它们在DC时有整体增益。可以容易地论证：新传递函数H' = 2-H，在DC时也是整体增益，且在DC时的组延迟具有与H相同的

幅值，但却是负值。如果你级联H和H'（即串联它们），你会得到一个整体传递函数，我们称其为H1，它具有DC整体增益和DC零组延时。对于S或Z域的任何线性传递函数来说，H1就等于HH'，即H1 = H(2-H)。无论哪类滤波器，只要H是可实现的，这也就可以实现。

这看起来似乎很怪诞。因为函数H'与H的阶相同（无论使用模拟或数字滤波器），你可以看到，将其组合起来会使滤波器的尺寸加倍，因此实现其所需的资源也要加倍。也许不太容易想象的是，它可能会大大降低滤波器的衰减性能。如果H是一个具有DC整体增益的低通函数，而在所有其它频率也具有整体增益（或小于整体增益），那么函数2-H就有一个会在1和3之间振荡的值，也就是说，它可以在响应中引入一个高达9.5dB的“凸点”。如果该凸点落于整体滤波器的阻带内，那么所发生的一切就只是衰减功能的恶化。如果凸点落在通带内，那么该级联的整个通带内的响应会与单个H时的大相径庭。

这里有个简单例子。对以100kps采样率数字方式实现的H，在10kHz时，以n=2的巴特沃斯滤波器开始。为了设计滤波器并获得图表，我使用了新版（2012年2月发布）的PSoC Creator滤波器工具，它为H给出了以下系数，幅度和组延时曲线在图1表示。

双二阶滤波器的最终系数：

系数序列为A0，A1，A2，B1和B2

0.0674552917480469

0.134910583496094

0.0674552917480469

-1.14298057556152

0.412801742553711


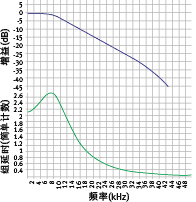
图1：0.01 Fs时，N=2的巴特沃斯滤波器的幅度和组延时。

补偿滤波器H'与H同分母，而分子等于两个负数（H的分子）。我用快速电子表格进行了计算，并将结果反馈给PSoC Creator滤波器工具。工具为这两个双二阶部分给出了最好的排序和增益；它获得了4dB增益，以确保凸点响应不高于0dB，见图2：

双二阶滤波器的最终系数：

系数序列为：A0，A1，A2，B1和B2

0.216065168380737

-0.2706618309021

0.0847635269165039

-1.14298057556152

0.412801742553711

0.372884273529053

0.745768547058105

0.372884273529053

-1.14298057556152

0.412801742553711


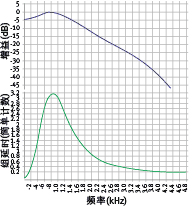
图2：带补偿滤波器的N=2巴特沃斯级联；零DC组延迟

在通带内，频率响应明显是非平坦（内有凹凸）的，而且已经放弃了一些相对阻带抑制。如果你熟悉控制系统理论，你马上会看到，我们得到的是增加的传递函数零，其组延时的贡献准确取消了原始的滤波器极点（以及新极点也会出现）。但它并非太过糟糕的一个响应——它仍能去掉数据序列的高频率噪声——如图3所示，某些神秘数据（哇!）：


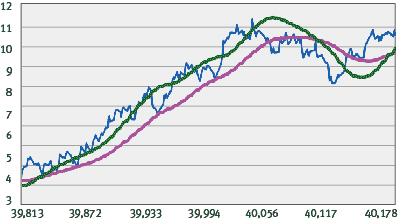
图3：某些数据（蓝色），巴特沃斯响应（粉红色）和补偿（绿色）

我们不必使用相同的函数H来构造补偿滤波器。如果两个传递函数HA和HB都具有整体单位DC增益和相同的DC组延迟值，则H1 =HA（2-HB）也有整体DC增益和零DC组延迟。

特别是，如果HB是T值的纯时间延迟（相等于HA的DC组延迟），我们可以得到FIR实现的漂亮简化。就T恰好等于N个采样周期的传递函数来说，我们得到H1 = HA（2-Z^- N），几乎所有的数字滤波器结构都能很容易地实现它，因为Z图的

这些负值直接作用于单位采样延迟。而2N+1阶的对称FIR滤波器总能满足该条件；如果多做点工作，它就可以适应不对称的情况，其中N不是整数。

因此，无论我们选择工作在S域或Z域，我们都可以构建零DC组延时的低通传递函数。但我们没必要在零组延时停止；虽然我们可以很容易地使其为负，我们也在此进入预测域。在采样系统中，有一个其输出是输入信号在下一个采样时刻可以预测的滤波器，会很方便。换句话说，一个滤波器的DC组延迟是负一个采样周期。在上面提到的FIR的情况，它简单得几乎难以置信。我们只须使用2-z^-(N+1)，而不是2-z^-N的补偿函数。

现在，如果在有能量进入滤波器之前，它就实际输出了一些能量，那就破坏了因果律。所以包含信息的任何信号不可能以负延迟的形式出现在输出。但有些信号不包含任何信息——如果一些观察家对其有心理上的期盼，则无论他们怎么想

——所以当组延迟为负时，就没有因果关系可去违反。