带曲率补偿、工作电压1.2 V、可调带隙基准电压电路
时间:10-23
来源:互联网
点击:
1 与温度无关的基准
与温度无关的电压或电流基准在许多模拟电路中是必不可少的。如何产生一个对温度变化保持恒定的量?假设有正温度系数的电压V1和负温度系数的电压V2,这两个量以适当的权重相加,那么结果就会显示出零温度系数。选取a和b使得aV1/ T+bv2/ T=0,可以得到具有零温度系数的电压基准,VREF=aV1+bV2。
上述假设提供了一个可行的方法实现与温度无关的电压基准,就是分别找到正温度系数的电压和负温度系数的电压。
1.1 负温度系数电压
双极晶体管的基极一发射极电压VBE或者pn结二极管的正向电压,具有负温度系数。根据已推导的VBE温度系数表达式:

式(1)给出了在给定温度T下VBE的温度系数,大小与VBE本身有关。其中VT为热电压,Eg为Si的带隙能量,m为迁移率的温度指数。根据经验值,当VBE△750 mV,T=300 K时,VBE/T△-1.5 mV/℃。当然这些参数必须以实际所用的工艺库为标准。
1.2 正温度系数电压
如果两个双极晶体管工作在不相等的电流密度下,那么他们的基极一发射极电压的差值就与绝对温度成正比。
假设两个相同的晶体管(Is1=Is2),基极和集电极分别短接,发射极接地,偏置的集电极电流分别为Ic1=nI0和Ic2=I0,其中n是晶体管Q2和Q1,的发射极面积比,忽略他们的基极电流,那么:
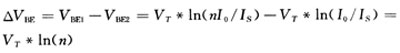
△VBE表现出正温度系数:
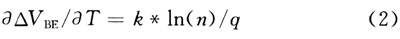
1.3 带隙基准
利用上述的负温度系数电压和正温度系数电压,可以设计出一个理想的零温度系数基准。
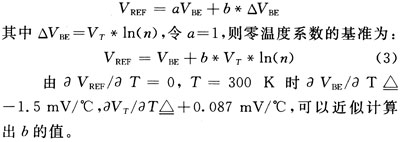
2 常规电路
通过上述分析,我们知道带隙基准由两个部分组成,一部分是晶体管的偏置,另一部分是与绝对温度成比例的电压(Proportional to the Absolute Temperature,PTAT)。正负温度系数电压刚好相互抵消。衡量带隙基准电压性能一般采用两个参数,温度系数(Temperature Coefficient,TC)和电源电压抑制比(Power Supply Rejection Ratio,PSRR)。
图1所示为常规带隙基准电压电路。
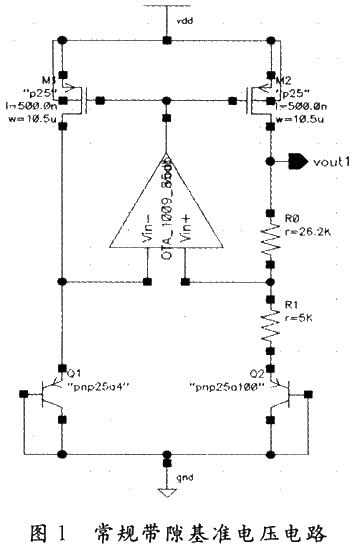
设运放Vin-和Vin+相应的节点为A和B,根据理想运放输入两端虚断的特点:
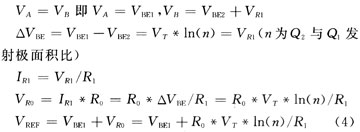
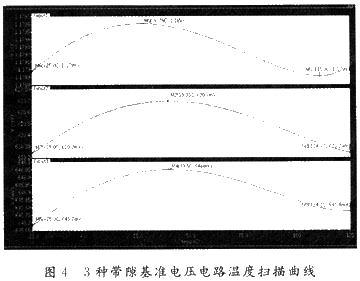
式(4)就是由常规电路得到的带隙基准电压VREF。在2.5 V工作电压,进行-25~125℃温度扫描,从扫描结果(图4中Voutl)可以看到,该电路得到的VREF大概在1.2 V左右,温度系数TC=5.65 ppm/℃。对电源电压进行2~3 V扫描,VREF从1.18 V变化到1.179 V,电源电压抑制比PSRR=55.4 dBo该电路的温度系数还不够理想,而且VREF不可调节,因此在常规电路的基础上进行改进。
3 改进电路
由于常规电路的温度系数还不够理想,而且VREF不可调节,因此改进常规电路。图2是文献提到的改进电路。

分析该电路,同样设运放Vin-和Vin+相应的节点为A和B,根据理想运放输入两端虚断的特点:
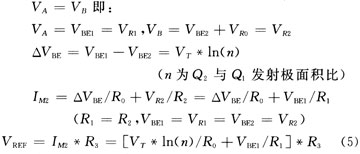
式(5)就是改进电路得到的带隙基准电压VREF。设R。=10 kΩ,通过VREF/ T=0,n=25,T=300 K时 VBE/T△-1.5 mV/℃和 VT/ T△+0.087 mV/℃,可以计算出R1和R2的近似值。在2.5 V工作电压,进行-25~125℃温度扫描,从扫描结果(图4中Vout2),可以计算出改进电路的温度系数TC=5.37 ppm/℃。对电源电压进行2~3 V扫描,VREF从62l.2 mV变化到620.5 mV,电源电压抑制比PSRR=52.9 dB。VREF可以通过改变R2的阻值进行调节,可调节范围约为O~2.25 V,实际应用中,考虑电阻在工艺上的误差,R3不宜取太小的阻值,因此VREF很难取到较小但又要求比较准确的电压,同时为了保证输出支路的PMOS管工作饱和区,所以合适的调节范围约为O.5~2 V。从计算结果发现改进电路的温度系数5.37 ppm/℃与常规电路的温度系数5.65 ppm/℃相比没有得到较大改善,因此电路还需改进。
4 曲率补偿的带隙基准电压电路
在实际情况下,VBF并不是像我们前面分析电路工作时所认为的是与温度成线性变化的关系。根据文献提到的经验公式:
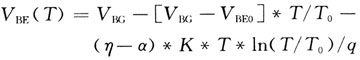
其中η是取决于双极性结构的参数,约为4,而a,当双极型晶体管电流与绝对温度成比例变化时,a为1,当电流与温度无关时,a为0。
前面两种电路分析过程都没有考虑VBE的非线性项引入的误差,为了得到更好的温度系数,必须对非线性项进行补偿。基本的补偿方法是校正非线性项,减去含有恒定电流的结产生的VBE和含有与绝对温度成比例变化电流的结产生的VBE。从图2我们看到IQ1与绝对温度成比例变化,IM2与温度无关。因此,如果将IM2镜像并注入到一个与双极型晶体管相连接的二极管,可以产生带恒定电流的VBE。完整曲率补偿的带隙基准电路如图3所示。R6和R7分别从M1和M2获得额外的电流,该电流与上述两种不同电流成比例。适当调整R6和R7的阻值可以实现预期的曲率补偿。
图3电路仅用两个电阻的补偿方法,比文献采用的方法要有效得多,而且比文献采用的方法要简单得多,因为文献采用运放,而文献采用开关电容结构。
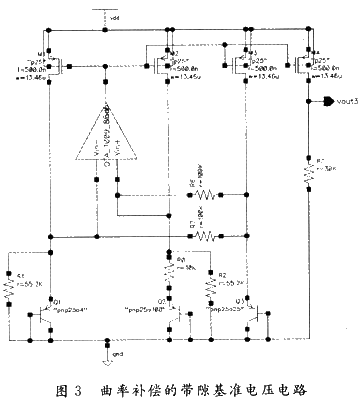
分析上述3种电路,并且用Cadence的仿真工具Spectre,SMIC标准0.25μm工艺,对上述3种电路进行仿真,图4就是3种电路在工作电压2.5 V,-25~125℃条件下的仿真结果。带曲率补偿的带隙基准电压电路,从温度扫描结果(图4中Vout3),可以计算出温度系数TC=3.10 ppm/℃。对电源电压进行2~3 V扫描,VREF从646.5 mV变化到645.9 mV,PSRR=54.6 dB。结果证明图3曲率补偿的带隙基准电压电路在温度系数上要优于其他两种电路。
通过标识3种带隙基准电压电路各个支路的电流,计算3种电路在2.5 V下的功耗,分别为0.72l mW,O.799 mW和0.859 mW。
与温度无关的电压或电流基准在许多模拟电路中是必不可少的。如何产生一个对温度变化保持恒定的量?假设有正温度系数的电压V1和负温度系数的电压V2,这两个量以适当的权重相加,那么结果就会显示出零温度系数。选取a和b使得aV1/ T+bv2/ T=0,可以得到具有零温度系数的电压基准,VREF=aV1+bV2。
上述假设提供了一个可行的方法实现与温度无关的电压基准,就是分别找到正温度系数的电压和负温度系数的电压。
1.1 负温度系数电压
双极晶体管的基极一发射极电压VBE或者pn结二极管的正向电压,具有负温度系数。根据已推导的VBE温度系数表达式:

式(1)给出了在给定温度T下VBE的温度系数,大小与VBE本身有关。其中VT为热电压,Eg为Si的带隙能量,m为迁移率的温度指数。根据经验值,当VBE△750 mV,T=300 K时,VBE/T△-1.5 mV/℃。当然这些参数必须以实际所用的工艺库为标准。
1.2 正温度系数电压
如果两个双极晶体管工作在不相等的电流密度下,那么他们的基极一发射极电压的差值就与绝对温度成正比。
假设两个相同的晶体管(Is1=Is2),基极和集电极分别短接,发射极接地,偏置的集电极电流分别为Ic1=nI0和Ic2=I0,其中n是晶体管Q2和Q1,的发射极面积比,忽略他们的基极电流,那么:
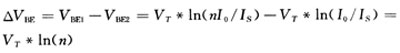
△VBE表现出正温度系数:
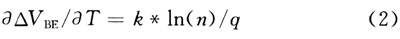
1.3 带隙基准
利用上述的负温度系数电压和正温度系数电压,可以设计出一个理想的零温度系数基准。
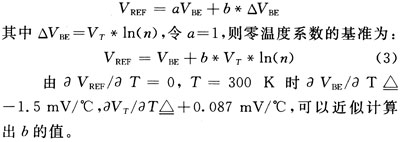
2 常规电路
通过上述分析,我们知道带隙基准由两个部分组成,一部分是晶体管的偏置,另一部分是与绝对温度成比例的电压(Proportional to the Absolute Temperature,PTAT)。正负温度系数电压刚好相互抵消。衡量带隙基准电压性能一般采用两个参数,温度系数(Temperature Coefficient,TC)和电源电压抑制比(Power Supply Rejection Ratio,PSRR)。
图1所示为常规带隙基准电压电路。

设运放Vin-和Vin+相应的节点为A和B,根据理想运放输入两端虚断的特点:
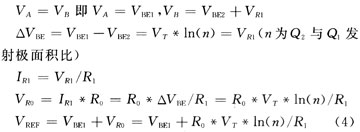
式(4)就是由常规电路得到的带隙基准电压VREF。在2.5 V工作电压,进行-25~125℃温度扫描,从扫描结果(图4中Voutl)可以看到,该电路得到的VREF大概在1.2 V左右,温度系数TC=5.65 ppm/℃。对电源电压进行2~3 V扫描,VREF从1.18 V变化到1.179 V,电源电压抑制比PSRR=55.4 dBo该电路的温度系数还不够理想,而且VREF不可调节,因此在常规电路的基础上进行改进。
3 改进电路
由于常规电路的温度系数还不够理想,而且VREF不可调节,因此改进常规电路。图2是文献提到的改进电路。

分析该电路,同样设运放Vin-和Vin+相应的节点为A和B,根据理想运放输入两端虚断的特点:
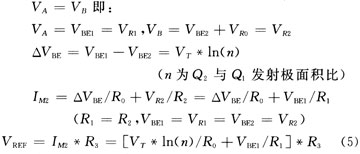
式(5)就是改进电路得到的带隙基准电压VREF。设R。=10 kΩ,通过VREF/ T=0,n=25,T=300 K时 VBE/T△-1.5 mV/℃和 VT/ T△+0.087 mV/℃,可以计算出R1和R2的近似值。在2.5 V工作电压,进行-25~125℃温度扫描,从扫描结果(图4中Vout2),可以计算出改进电路的温度系数TC=5.37 ppm/℃。对电源电压进行2~3 V扫描,VREF从62l.2 mV变化到620.5 mV,电源电压抑制比PSRR=52.9 dB。VREF可以通过改变R2的阻值进行调节,可调节范围约为O~2.25 V,实际应用中,考虑电阻在工艺上的误差,R3不宜取太小的阻值,因此VREF很难取到较小但又要求比较准确的电压,同时为了保证输出支路的PMOS管工作饱和区,所以合适的调节范围约为O.5~2 V。从计算结果发现改进电路的温度系数5.37 ppm/℃与常规电路的温度系数5.65 ppm/℃相比没有得到较大改善,因此电路还需改进。
4 曲率补偿的带隙基准电压电路
在实际情况下,VBF并不是像我们前面分析电路工作时所认为的是与温度成线性变化的关系。根据文献提到的经验公式:
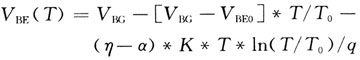
其中η是取决于双极性结构的参数,约为4,而a,当双极型晶体管电流与绝对温度成比例变化时,a为1,当电流与温度无关时,a为0。
前面两种电路分析过程都没有考虑VBE的非线性项引入的误差,为了得到更好的温度系数,必须对非线性项进行补偿。基本的补偿方法是校正非线性项,减去含有恒定电流的结产生的VBE和含有与绝对温度成比例变化电流的结产生的VBE。从图2我们看到IQ1与绝对温度成比例变化,IM2与温度无关。因此,如果将IM2镜像并注入到一个与双极型晶体管相连接的二极管,可以产生带恒定电流的VBE。完整曲率补偿的带隙基准电路如图3所示。R6和R7分别从M1和M2获得额外的电流,该电流与上述两种不同电流成比例。适当调整R6和R7的阻值可以实现预期的曲率补偿。
图3电路仅用两个电阻的补偿方法,比文献采用的方法要有效得多,而且比文献采用的方法要简单得多,因为文献采用运放,而文献采用开关电容结构。

分析上述3种电路,并且用Cadence的仿真工具Spectre,SMIC标准0.25μm工艺,对上述3种电路进行仿真,图4就是3种电路在工作电压2.5 V,-25~125℃条件下的仿真结果。带曲率补偿的带隙基准电压电路,从温度扫描结果(图4中Vout3),可以计算出温度系数TC=3.10 ppm/℃。对电源电压进行2~3 V扫描,VREF从646.5 mV变化到645.9 mV,PSRR=54.6 dB。结果证明图3曲率补偿的带隙基准电压电路在温度系数上要优于其他两种电路。
通过标识3种带隙基准电压电路各个支路的电流,计算3种电路在2.5 V下的功耗,分别为0.72l mW,O.799 mW和0.859 mW。

电压 电流 模拟电路 二极管 电路 电阻 电容 Cadence 仿真 相关文章:
- 选择最佳的电压基准源(11-29)
- 对电压参考进行滤波以获得低噪声性能(01-16)
- 可编程快速充电管理芯片MAX712/ MAX713及其应用(01-23)
- 改进型全桥移相ZVS-PWMDC/DC变换器(01-23)
- 负输出罗氏变换器实用性剖析(01-09)
- 通信电源设备对杂音电压的控制要求(02-13)
