子网络级模拟故障诊断的神经网络实现
时间:07-25
来源:互联网
点击:
1 引 言
模拟电路故障诊断自20世纪60年代开始研究以来,已取得很多成就,提出了故障字典法、故障验证法、参数辨识法及网络撕裂法等。
从自动测试的角度来讲,一个好的诊断方法应该具有较少的测试点、较小的测后计算量、较高的故障定位率,而且对容差和测量误差的鲁棒性好并能测试软故障等。但到目前为止,上述诊断方法中没有一种能满足所有这些要求。故障字典法因其所需测试点少,适用于各种类型的电路,被认为是目前能较好地应用于实际电路诊断的有效方法,但他只能诊断硬故障,且随着故障状态增多测后计算量急剧增加。通过算法的改进来提高诊断速度必然是有限的,因此当神经网络兴起后,很多学者借助其高速并行信息处理能力从根本上解决字典法因测后计算量大而无法实用的问题,并取得了很多成就。这些方法大部分都把研究的重点放在神经网络算法的改进上,对训练样本特征的研究较少,即使考虑了优选训练样本,也没有对软、硬故障的样本特征进行深入研究。本文通过对元件软、硬故障的测量数据进行分析,找到了他们之间的共同性,从而把元件软、硬故障数据统一成一个样本数据,然后用于子网络级故障诊断,既大大减少了训练样本的数量,又提高了训练速度和诊断精度。
2 元件软、硬故障特征统一性
设节点a,b,c为待测电路N的可及点,当电路中任一元件参数Xi的变化为△Xi时,由此而引起的节点电压Va,Vb,Vc的改变量分别为△Va,△Vb,△Vc。由容差模拟电路节点电压灵敏度序列守恒定理可知,|△Va|,|△Vb|,|△Vc|的大小关系不随Xi的变化而改变,且有:
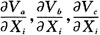 分别为a,b,c三点的节点电压对参数Xi的灵敏度。
分别为a,b,c三点的节点电压对参数Xi的灵敏度。
当参数Xi发生不同的变化时,对待测电路进行第i次测量和第j次测量得到a,b,c三点的电压改变量分别为△Vai,△Vbi,△Vci和△Vaj,△Vbj,△Vcj,他们间有如下关系:
3 诊断实例
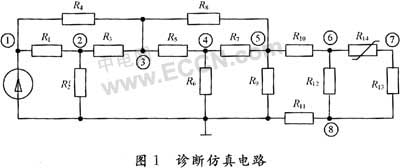
电路如图1所示,其中R14为非线性元件,R1=R3=R6=R10=2 kΩ;R4=R9=R12=510 Ω;R2=R8=R11=R13=1 kΩ;R5=R7=200 Ω,线性元件容差均为±5%;电路中节点1,3,5,6,8可及,在节点3,5,0处将电路撕裂为3个子网络。
3.1 原始数据集的产生
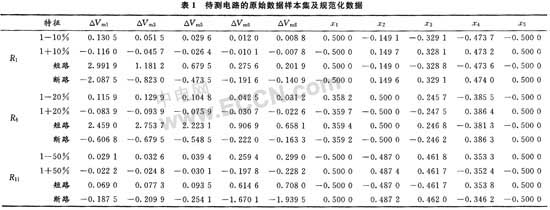
对图示电路,在节点1施加10 mA的直流激励,取全部可及点作为测试点,对各元件故障情况进行仿真。所得数据见表1,其中只列出其中3个元件部分代表性数据。
3.2 数据分析及预处理
在取得了原始数据后,需进行数据的分析及预处理,目的是使变换后的数据特征更为突出,而且数据更易于神经网络的学习和训练。通过对原始数据的观察和计算,可以证明不论参数发生什么变化,节点电压改变量之间的相对变化量是恒定的,即元件的软、硬故障特征是统一的。同时,为了便于神经网络的学习和训练,还需对数据进行尺度变换。
令BP网络的输入特征向量为:
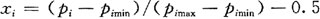
xi为经尺度变换后的第i个输入特征值;
Pi为原始数据中的第i次测量值;
Pimin为原始数据第i次测量值中的最小值;
pimax为原始数据第i次测量值中的最大值。
经过如上的规范化处理后,对各待测状态,其特征向量的每个分量都被规范化在闭区间[=0.5,0.5]内。因此,神经网络的输入范围对原点对称。经过规范化处理后的数据也列在表1中,这些数据的绝对值几乎相等,进一步验证了上述结论。
3.3 统一样本集的构造
由于同一元件在不同故障状态下的输入特征相同,所以只选取每个元件的一种故障状态信息构成神经网络的训练样本集,从而使得训练样本数量大大减少,加快了训练的速度。
3.4 神经网络的训练与测试
选各元件对应的故障特征向量作为BP网络的输入样本,并令网络输出代表待测的子网络。这样,网络的输入层为5个结点,输出层为3个结点。对于隐层,根据Kol-mogorov定理:对于任意连续的函数φ,可以用一个三层网络来精确地实现他,网络的输入层有m个单元,隐层有2m+1个单元,输出层有n个单元。确定隐层结点数的理论值后,再通过试凑法对(L-δ,L+δ)区间内的数值进行仿真对比(其中δ∈N,L为理论隐层结点数),从而得出神经网络模型的最终隐层结点数。根据上面的叙述,可以确定网络的隐层结点数理论值为11。为了得到最终的隐结点数,按照Kolmogorov定理,分别设置网络隐结点数为9,11,13,经过训练时间、精度等方面的比较,最终确定隐结点数为13。
经过规范化处理后,训练样本的数量大大减少,所以采用批处理法进行网络的训练。对应每一故障元件的测试数据,只选择其中的两个作为样本数据,一个为元件参数增大方向的数据,另一个为参数减小方向的数据,他们分别对应相应子网络的KCL值大于零(取值为0.5)和小于零(取值为-0.5)两种情况。子网络正常时,期望输出为0(容差情况下输出值介于±0.5之间);子网络故障时输出为0.5(或-0.5)。训练时,采用标准BP算法。训练结束后,对网络进行测试。
测试时选取了85个故障数据,BP网络对其中80个故障诊断正确,5个错误,正确率为94%。这里需要指出的是,利用标准BP神经网络对待测电路的所有可能故障(包括软故障和硬故障)进行诊断,通过对诊断结果的观察发现,网络对大部分元件(包括非线性元件)的软、硬故障的诊断正确率几乎为100%,误诊断集中在元件R2,R3故障时导致的子网络1故障。经过分析发现,当R2,R3故障时,子网络1的KCL方程值有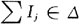 成立,因此被误诊断,重新选择对R2,R3灵敏度较高的节点作为可及点能改善诊断效果。
成立,因此被误诊断,重新选择对R2,R3灵敏度较高的节点作为可及点能改善诊断效果。
模拟电路故障诊断自20世纪60年代开始研究以来,已取得很多成就,提出了故障字典法、故障验证法、参数辨识法及网络撕裂法等。
从自动测试的角度来讲,一个好的诊断方法应该具有较少的测试点、较小的测后计算量、较高的故障定位率,而且对容差和测量误差的鲁棒性好并能测试软故障等。但到目前为止,上述诊断方法中没有一种能满足所有这些要求。故障字典法因其所需测试点少,适用于各种类型的电路,被认为是目前能较好地应用于实际电路诊断的有效方法,但他只能诊断硬故障,且随着故障状态增多测后计算量急剧增加。通过算法的改进来提高诊断速度必然是有限的,因此当神经网络兴起后,很多学者借助其高速并行信息处理能力从根本上解决字典法因测后计算量大而无法实用的问题,并取得了很多成就。这些方法大部分都把研究的重点放在神经网络算法的改进上,对训练样本特征的研究较少,即使考虑了优选训练样本,也没有对软、硬故障的样本特征进行深入研究。本文通过对元件软、硬故障的测量数据进行分析,找到了他们之间的共同性,从而把元件软、硬故障数据统一成一个样本数据,然后用于子网络级故障诊断,既大大减少了训练样本的数量,又提高了训练速度和诊断精度。
2 元件软、硬故障特征统一性
设节点a,b,c为待测电路N的可及点,当电路中任一元件参数Xi的变化为△Xi时,由此而引起的节点电压Va,Vb,Vc的改变量分别为△Va,△Vb,△Vc。由容差模拟电路节点电压灵敏度序列守恒定理可知,|△Va|,|△Vb|,|△Vc|的大小关系不随Xi的变化而改变,且有:
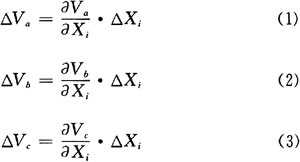
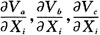 分别为a,b,c三点的节点电压对参数Xi的灵敏度。
分别为a,b,c三点的节点电压对参数Xi的灵敏度。当参数Xi发生不同的变化时,对待测电路进行第i次测量和第j次测量得到a,b,c三点的电压改变量分别为△Vai,△Vbi,△Vci和△Vaj,△Vbj,△Vcj,他们间有如下关系:
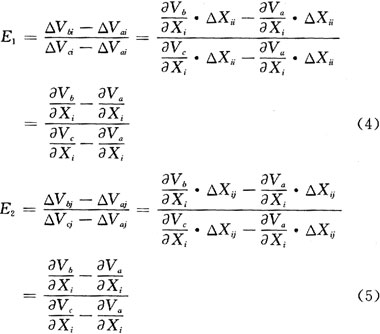
3 诊断实例
电路如图1所示,其中R14为非线性元件,R1=R3=R6=R10=2 kΩ;R4=R9=R12=510 Ω;R2=R8=R11=R13=1 kΩ;R5=R7=200 Ω,线性元件容差均为±5%;电路中节点1,3,5,6,8可及,在节点3,5,0处将电路撕裂为3个子网络。
3.1 原始数据集的产生
对图示电路,在节点1施加10 mA的直流激励,取全部可及点作为测试点,对各元件故障情况进行仿真。所得数据见表1,其中只列出其中3个元件部分代表性数据。
3.2 数据分析及预处理
在取得了原始数据后,需进行数据的分析及预处理,目的是使变换后的数据特征更为突出,而且数据更易于神经网络的学习和训练。通过对原始数据的观察和计算,可以证明不论参数发生什么变化,节点电压改变量之间的相对变化量是恒定的,即元件的软、硬故障特征是统一的。同时,为了便于神经网络的学习和训练,还需对数据进行尺度变换。
令BP网络的输入特征向量为:
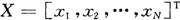
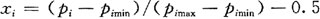
xi为经尺度变换后的第i个输入特征值;
Pi为原始数据中的第i次测量值;
Pimin为原始数据第i次测量值中的最小值;
pimax为原始数据第i次测量值中的最大值。
经过如上的规范化处理后,对各待测状态,其特征向量的每个分量都被规范化在闭区间[=0.5,0.5]内。因此,神经网络的输入范围对原点对称。经过规范化处理后的数据也列在表1中,这些数据的绝对值几乎相等,进一步验证了上述结论。
3.3 统一样本集的构造
由于同一元件在不同故障状态下的输入特征相同,所以只选取每个元件的一种故障状态信息构成神经网络的训练样本集,从而使得训练样本数量大大减少,加快了训练的速度。
3.4 神经网络的训练与测试
选各元件对应的故障特征向量作为BP网络的输入样本,并令网络输出代表待测的子网络。这样,网络的输入层为5个结点,输出层为3个结点。对于隐层,根据Kol-mogorov定理:对于任意连续的函数φ,可以用一个三层网络来精确地实现他,网络的输入层有m个单元,隐层有2m+1个单元,输出层有n个单元。确定隐层结点数的理论值后,再通过试凑法对(L-δ,L+δ)区间内的数值进行仿真对比(其中δ∈N,L为理论隐层结点数),从而得出神经网络模型的最终隐层结点数。根据上面的叙述,可以确定网络的隐层结点数理论值为11。为了得到最终的隐结点数,按照Kolmogorov定理,分别设置网络隐结点数为9,11,13,经过训练时间、精度等方面的比较,最终确定隐结点数为13。
经过规范化处理后,训练样本的数量大大减少,所以采用批处理法进行网络的训练。对应每一故障元件的测试数据,只选择其中的两个作为样本数据,一个为元件参数增大方向的数据,另一个为参数减小方向的数据,他们分别对应相应子网络的KCL值大于零(取值为0.5)和小于零(取值为-0.5)两种情况。子网络正常时,期望输出为0(容差情况下输出值介于±0.5之间);子网络故障时输出为0.5(或-0.5)。训练时,采用标准BP算法。训练结束后,对网络进行测试。
测试时选取了85个故障数据,BP网络对其中80个故障诊断正确,5个错误,正确率为94%。这里需要指出的是,利用标准BP神经网络对待测电路的所有可能故障(包括软故障和硬故障)进行诊断,通过对诊断结果的观察发现,网络对大部分元件(包括非线性元件)的软、硬故障的诊断正确率几乎为100%,误诊断集中在元件R2,R3故障时导致的子网络1故障。经过分析发现,当R2,R3故障时,子网络1的KCL方程值有
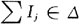 成立,因此被误诊断,重新选择对R2,R3灵敏度较高的节点作为可及点能改善诊断效果。
成立,因此被误诊断,重新选择对R2,R3灵敏度较高的节点作为可及点能改善诊断效果。- 0.5μm CMOS带隙基准电路设计(01-13)
- 使用开关电源的问题总结(02-20)
- 模拟电路故障诊断中的特征提取方法(03-03)
- 基于BP神经网络的模拟电路诊断系统研究(04-07)
- 基于Multisim的差分放大电路仿真分析(06-14)
- 容差模拟电路的软故障诊断的小波方法(10-03)
