ADC信噪比的分析及高速高分辨率ADC电路实现
时间:07-05
来源:互联网
点击:
在雷达、导航等军事领域中,由于信号带宽宽(有时可能高于10MHz),要求ADC的采样率高于30MSPS,分辨率大于10位。目前高速高分辨率ADC器件在采样率高于10MSPS时,量化位数可达14位,但实际分辨率受器件自身误差和电路噪声的影响很大。在数字通信、数字仪表、软件无线电等领域中应用的高速ADC电路,在输入信号低于1MHz时,实际分辨率可达10位,但随输入信号频率的增加下降很快,不能满足军事领域的使用要求。
针对这一问题,本文主要研究在不采用过采样、数字滤波和增益自动控制等技术条件下,如何提高高速高分辨率ADC电路的实际分辨率,使其最大限度地接近ADC器件自身的实际分辨率,即最大限度地提高ADC电路的信噪比。为此,本文首先从理论上分析了影响ADC信噪比的因素;然后从电路设计和器件选择两方面出发,设计了高速高分辨率ADC电路。经实测表明,当输入信号频率为0.96MHz时,该电路的实际分辨率为11.36位;当输入信号频率为14.71MHz日寸,该电路的实际分辨率为10.88位。
1 影响ADC信噪比因素的理论分析
ADC的实际分辨率是用有效位数ENOB标称的。不考虑过采样,当满量程单频理想正弦波输入时,实际分辨率可用下式表示:
ENOB=[SINA0(dB)-1.76]/6.02 (1)
式中,SINAD表示ADC的信噪失真比,指ADC满量程单频理想正弦波输入信号的有效值与ADC输出信号的奈奎斯特带宽内的全部其它频率分量(包括谐波分量,但不包括直流允量)的总有效值之比。
ADC的信噪比SNR,指ADC满量程单频理想正弦波输入信号的有效值与ADC输出信号的奈奎斯特带宽内的全部其它频率分量(不包括直流分量和谐波分量)总有效值之比。
由此可知,当ADC的总谐波失真THD一定时,有效位数ENOB取决于SNR;ADC的SNR越高,其有效位数ENOB就越高。下面就来分析影响ADC信噪比SNR的因素。
理想ADC的噪声由其固有的量化误差(也称为量化噪声,如图1所示)产生。但实际使用的ADC是非理想器件,它的实际转换曲线与理想转换曲线之间存在偏差,表现为多种误差,如零点误差、满度误差、增益误差、积分非线性误差INL、微分非线性误差DNL等。其中,零点误差、满度误差、增益误差是恒定误差,只影响ADC的绝对精度,不影响ADC的SNR。INL指的是在校准上述恒定误差的基础上,ADC实际转换曲线与理想转换曲线的最大偏差。而DNL指的是ADC实际量化间隔与理想量化间隔的最大偏差,改变ADC的量化误差,能更直接地计算出ADC实际转换曲线与理想转换曲线的偏差对ADC的SNR的影响。
非理想ADC,除了上述误差外,还有各种噪声,如热噪声、孔径抖动。前者是由半导体器件内部分子热运动产生的,后者是由ADC孔径延时的不确定性造成的。而ADC的外围电路同样会带来噪声,如ADC输入级电路的热噪声、电源/地线上的杂波、空间电磁波干扰、外接时钟的不稳定性(导致ADC各采样时钟沿出现时刻不确定,带来孔径抖动)等,可以把它们都等效为ADC的上述两种内部噪声。
上述误差和噪声的存在,导致ADC的SNR下降。下面先给出理想ADC的SNR计算公式,然后具体分析微分非线性误差DNL、孔径抖动△tj和热噪声对ADC的SNR的影响。
1.1 理想ADC的SNR
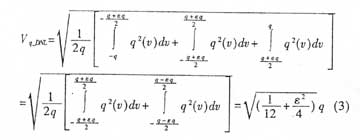
理想ADC的量化误差g(υ)与满量程内输入信号的电压V的关系如图1所示。量化误差为在[-q/2,q/2]内均匀分布且峰-峰值等于q(q=1LSB,LSB表示理想ADC的最小量化间隔)的锯齿波信号。
设N位ADC满量程电压为±1V,输入信号为s(t)=sinωt,则输入信号电压有效值Vs=1/√2=2N/2√2×q,量化噪声电压有效值于是得ADC输出信噪比为
SNR=6.02N+1.76(dB)
1.2 微分非线性误差DNL
非理想ADC的量化间隔是非等宽的,这将导致ADC器件不能完全正确地把模拟信号转化成相应的二进制码,从而造成SNR的下降;且ADC每个量化的二进制码所对应的量化间隔都不同,为便于分析,用ε(LSB)= εq表示实际量化间隔与理想量化间隔误差的有效值,并近似认为由于DNL的影响,在无失码条件(DNL<1LSB)下,量化误差均匀分布在[-上q+εq/2,q+εq/2]和[-q-εq/2,q-εq/2]内。如图1 中实线所示(虚线伪理想ADC量化误差)。这样,在考虑了DNL之后的ADC量化噪声电压Vq_DNL为:
1.3 孔径抖动△tj
孔径时间又称孔径延迟时间,是指对ADC发出采样命令(采样时钟边沿)时刻与实际开始采样时刻之间的时间间隔。相邻两次采样的孔径时间的偏差称为孔径抖动,记作△tj。孔径抖动造成了信号的非均匀采样,引起了误差,设ADC满量程电压为±1V输入信号为s(t)=sinωt,孔径抖动有效值为σ△tj,则由孔径抖动带来的误差电压为:

1.4 热噪声
这里将ADC电路中微分非线性误差DNL、孔径抖动△tj外的其它噪声都等效为ADC输入端的热噪声电压Vtn,设其有效值为σtn。
1.5 非理想ADC的SNR
一般情况下,量化噪声、微分非线性误差DNL、孔径抖动△tj和热噪声彼此相互独立,综合芍虑这四个因素的影响,可得到ADC的SNR计算公式如卡:
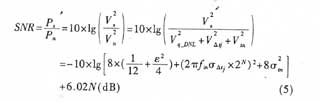
式中,N--ADC的量化位数
ε--ADC的实际量化间隔与理想量化间隔误差的有效值,单位LSB
fin--ADC输入信号频率,单位Hz
σ△tj--ADC的孑L径抖动有效值,单位s
σtn--等效到ADC输入端的热噪声的有效值单位LSB
对于高分辨率ADC器件,其固有量化误差、微分非线性误差DNL和器件热噪声均较小。当fin较高时,ADC电路的SNR主要取决于孔径抖动,此时有
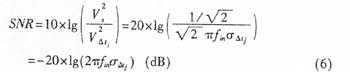
2 基于AD6644AST一65的高速高分辨率ADC电路设计实例
电路设计目标:有效位数ENOB≥10.50bit、采样率为40MSPS、输入信号频率小于15MHz,输入信号幅度为-ldBFs。该指标能满足数字仪表、高速数据采集卡、软件无线电和雷达、导航等领域中数字波束形成的要求。
2.1 电路设计与器件选择
本电路主要由模/数转换器ADC、输入电路、输出屯路、时钟电路和电源电路组成,如图2所示。
针对这一问题,本文主要研究在不采用过采样、数字滤波和增益自动控制等技术条件下,如何提高高速高分辨率ADC电路的实际分辨率,使其最大限度地接近ADC器件自身的实际分辨率,即最大限度地提高ADC电路的信噪比。为此,本文首先从理论上分析了影响ADC信噪比的因素;然后从电路设计和器件选择两方面出发,设计了高速高分辨率ADC电路。经实测表明,当输入信号频率为0.96MHz时,该电路的实际分辨率为11.36位;当输入信号频率为14.71MHz日寸,该电路的实际分辨率为10.88位。
1 影响ADC信噪比因素的理论分析
ADC的实际分辨率是用有效位数ENOB标称的。不考虑过采样,当满量程单频理想正弦波输入时,实际分辨率可用下式表示:
ENOB=[SINA0(dB)-1.76]/6.02 (1)
式中,SINAD表示ADC的信噪失真比,指ADC满量程单频理想正弦波输入信号的有效值与ADC输出信号的奈奎斯特带宽内的全部其它频率分量(包括谐波分量,但不包括直流允量)的总有效值之比。
ADC的信噪比SNR,指ADC满量程单频理想正弦波输入信号的有效值与ADC输出信号的奈奎斯特带宽内的全部其它频率分量(不包括直流分量和谐波分量)总有效值之比。
由此可知,当ADC的总谐波失真THD一定时,有效位数ENOB取决于SNR;ADC的SNR越高,其有效位数ENOB就越高。下面就来分析影响ADC信噪比SNR的因素。
理想ADC的噪声由其固有的量化误差(也称为量化噪声,如图1所示)产生。但实际使用的ADC是非理想器件,它的实际转换曲线与理想转换曲线之间存在偏差,表现为多种误差,如零点误差、满度误差、增益误差、积分非线性误差INL、微分非线性误差DNL等。其中,零点误差、满度误差、增益误差是恒定误差,只影响ADC的绝对精度,不影响ADC的SNR。INL指的是在校准上述恒定误差的基础上,ADC实际转换曲线与理想转换曲线的最大偏差。而DNL指的是ADC实际量化间隔与理想量化间隔的最大偏差,改变ADC的量化误差,能更直接地计算出ADC实际转换曲线与理想转换曲线的偏差对ADC的SNR的影响。
|
非理想ADC,除了上述误差外,还有各种噪声,如热噪声、孔径抖动。前者是由半导体器件内部分子热运动产生的,后者是由ADC孔径延时的不确定性造成的。而ADC的外围电路同样会带来噪声,如ADC输入级电路的热噪声、电源/地线上的杂波、空间电磁波干扰、外接时钟的不稳定性(导致ADC各采样时钟沿出现时刻不确定,带来孔径抖动)等,可以把它们都等效为ADC的上述两种内部噪声。
上述误差和噪声的存在,导致ADC的SNR下降。下面先给出理想ADC的SNR计算公式,然后具体分析微分非线性误差DNL、孔径抖动△tj和热噪声对ADC的SNR的影响。
1.1 理想ADC的SNR
理想ADC的量化误差g(υ)与满量程内输入信号的电压V的关系如图1所示。量化误差为在[-q/2,q/2]内均匀分布且峰-峰值等于q(q=1LSB,LSB表示理想ADC的最小量化间隔)的锯齿波信号。
设N位ADC满量程电压为±1V,输入信号为s(t)=sinωt,则输入信号电压有效值Vs=1/√2=2N/2√2×q,量化噪声电压有效值于是得ADC输出信噪比为
SNR=6.02N+1.76(dB)
1.2 微分非线性误差DNL
非理想ADC的量化间隔是非等宽的,这将导致ADC器件不能完全正确地把模拟信号转化成相应的二进制码,从而造成SNR的下降;且ADC每个量化的二进制码所对应的量化间隔都不同,为便于分析,用ε(LSB)= εq表示实际量化间隔与理想量化间隔误差的有效值,并近似认为由于DNL的影响,在无失码条件(DNL<1LSB)下,量化误差均匀分布在[-上q+εq/2,q+εq/2]和[-q-εq/2,q-εq/2]内。如图1 中实线所示(虚线伪理想ADC量化误差)。这样,在考虑了DNL之后的ADC量化噪声电压Vq_DNL为:

1.3 孔径抖动△tj
孔径时间又称孔径延迟时间,是指对ADC发出采样命令(采样时钟边沿)时刻与实际开始采样时刻之间的时间间隔。相邻两次采样的孔径时间的偏差称为孔径抖动,记作△tj。孔径抖动造成了信号的非均匀采样,引起了误差,设ADC满量程电压为±1V输入信号为s(t)=sinωt,孔径抖动有效值为σ△tj,则由孔径抖动带来的误差电压为:

1.4 热噪声
这里将ADC电路中微分非线性误差DNL、孔径抖动△tj外的其它噪声都等效为ADC输入端的热噪声电压Vtn,设其有效值为σtn。
1.5 非理想ADC的SNR
一般情况下,量化噪声、微分非线性误差DNL、孔径抖动△tj和热噪声彼此相互独立,综合芍虑这四个因素的影响,可得到ADC的SNR计算公式如卡:
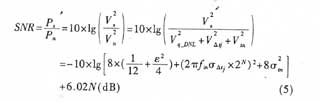
式中,N--ADC的量化位数
ε--ADC的实际量化间隔与理想量化间隔误差的有效值,单位LSB
fin--ADC输入信号频率,单位Hz
σ△tj--ADC的孑L径抖动有效值,单位s
σtn--等效到ADC输入端的热噪声的有效值单位LSB
对于高分辨率ADC器件,其固有量化误差、微分非线性误差DNL和器件热噪声均较小。当fin较高时,ADC电路的SNR主要取决于孔径抖动,此时有
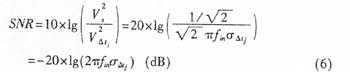
2 基于AD6644AST一65的高速高分辨率ADC电路设计实例
电路设计目标:有效位数ENOB≥10.50bit、采样率为40MSPS、输入信号频率小于15MHz,输入信号幅度为-ldBFs。该指标能满足数字仪表、高速数据采集卡、软件无线电和雷达、导航等领域中数字波束形成的要求。
2.1 电路设计与器件选择
本电路主要由模/数转换器ADC、输入电路、输出屯路、时钟电路和电源电路组成,如图2所示。
ADC 电路 无线电 半导体 电压 变压器 ADI 电容 电流 总线 电阻 Linear LDO 稳压电源 模拟电路 电感 信号发生器 滤波器 相关文章:
- 12位串行A/D转换器MAX187的应用(10-06)
- 低功耗、3V工作电压、精度0.05% 的A/D变换器(10-09)
- 12位串行A/D转换器的原理及应用开发(10-09)
- 在射击探测器中增加口径确定功能的简单电路(11-13)
- 一种折叠共源共栅运算放大器的设计(11-20)
- 深入解析:模拟前端模/数转换器的三种类型 (11-26)