正交频分复用系统中的频偏估计
时间:07-17
来源:互联网
点击:
的子载波间隔。这个子载波频偏可使频域上接收机已解调符号的第m个子载波比发射机的第m个子载波多乘一个因子e-j2π△fmt,即在频域上产生了一个相位旋转。由此可见,若没有ISI的影响,就可以通过对采样时钟偏移(△F0=F0'-F0)和小数倍频偏(△f0=f0-f0)所产生的相位之和进行联合估计。
一个符号中连续导频的位置是固定不变的,当前后两个符号的对应导频点相关时,就会得到前后两个符号对应导频点的小数倍频偏和采样时钟频偏所产生的相位差,该相位差可表示为:
如果设
2.3 仿真分析
笔者在瑞利衰落信道下对上述频率偏移估计方法进行仿真,对于频偏设置为0.1倍的子载波间隔,采样钟频率偏移为100 ppm,若以L为保护间隔长度,N=2048为一个符号的数据长度,其频偏估计性能曲线如图3所示。
3 结束语
从图3可以看出,估计误差小于0.01倍的载波隔要求的信噪比比较低,因此该算法完全能满足OFDM系统性能的要求。
一个符号中连续导频的位置是固定不变的,当前后两个符号的对应导频点相关时,就会得到前后两个符号对应导频点的小数倍频偏和采样时钟频偏所产生的相位差,该相位差可表示为:
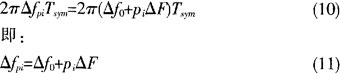
如果设

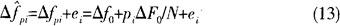
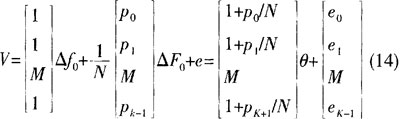

2.3 仿真分析
笔者在瑞利衰落信道下对上述频率偏移估计方法进行仿真,对于频偏设置为0.1倍的子载波间隔,采样钟频率偏移为100 ppm,若以L为保护间隔长度,N=2048为一个符号的数据长度,其频偏估计性能曲线如图3所示。

3 结束语
从图3可以看出,估计误差小于0.01倍的载波隔要求的信噪比比较低,因此该算法完全能满足OFDM系统性能的要求。
仿真 相关文章:
- 一种基于OPNET的小型网络仿真及分析(04-08)
- APOX软件在A+B频段无线网络规划中的应用(06-26)
- 基于GUI的跳频OFDM系统仿真设计(03-03)
- 基于CPLD的RS-232串口通信实现(04-23)
- 2.5 Gbps收发器中1∶2解复用电路的设计(09-17)
- 填补网络 SoC 设计前端与后端验证的差距(09-19)
