正交频分复用系统中的频偏估计
时间:07-17
来源:互联网
点击:
0 引言
正交频分复用(Orthogonal Frequency DivisionMultiplexing,OFDM)具有高速传输数据、高效的频谱利用率和抗多径的能力。最近几年,OFDM技术已经成功地应用在移动以及固定数据传输中,例如非对称数字用户线路(Asymmetric Digi-tal Subscriber Line,ADSL)、数字视频广播(DVB-T和DVB-H),以及无线局域网(WirelessLAN)等。目前,OFDM已被视为第四代移动通信最具竞争力的传输技术。由于OFDM在频域把信道分成许多正交子信道,各子信道的载波间保持正交,且频谱相互重叠,这样就减小了子信道间的干扰,提高了频谱利用率。所以,OFDM系统对频率偏移非常敏感,很小的频率偏移都可能破坏子载波间的正交性,从而产生载波间干扰(ICI)以造成系统性能的严重下降。因此,在OFDM系统中,频率偏移估计的准确性至关重要。
1 OFDM系统及其同步要求
OFDM系统能有效地对抗信道多径衰落;它通过将串行数据流调制到并行的子载波上,可在很大程度上提高带宽利用率;而在传输的数据流码字中插入循环前缀(CP),则能够有效地消除码间干扰和载波间干扰。图1所示是OFDM系统的简单结构。
该技术首先对输入信号流进行调制(例如PSK或QAM),以将数据流通过IDFT调制到N个子载波上,然后经过IDFT使每个符号的后L个抽样被复制到符号前端以形成循环前缀,再经过信道传输,并在接收端除去循环前缀,接着将接收到的符号经过DFT变换,这样就能恢复传输信号。在信道上传输的信号可能会受到噪声干扰,这是因为接收端和发送端的频率不匹配,此外,多普勒频移也会产生频率偏移。如不考虑信道衰落的影响,接收符号和发送符号之间的关系如下:
2 频率同步算法
由Jan-Japp提出的最大似然估计(ML)算法具有计算量小、冗余度低、算法实现简单、可同时估计定时和频偏的优点。但该算法的频率估计范围过小,定时估计较为粗糙,不能直接用到实际系统中。由ML算法估计的实际相对频差为:
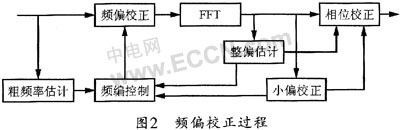
频偏估计时通常将频率偏移划分成分数部分和整数部分。这里是以子载波间隔作为归一化标准。子载波间隔的整数倍的频偏称为整数部分频偏,剩余的小于一个子载波问隔的频偏称为分数部分频偏。整数频偏经IFFT变换后通常表现成对应子载波标号的偏移,而分数倍频偏则表现为相位的旋转。由于OFDM系统存在大量的提升功率的导频,因此,只要搜索到这些导频就可以得到整数倍频率偏移,而检测导频的相位又可以得到分数倍频偏。估计到的频率误差除了要送到后一级以实时纠正数据的相位外,为了减小载波间干扰,还必须将其前馈到时域进行频率校正,因此频偏的校正示意图可用图2来说明。
2.1 整数倍频偏估计
一般来说,整数倍频率同步的作用是对频率整数倍子载波间隔部分进行估计。没有频偏时的频域信号Y(k)=FFT(y(n))=FFT(x(n)),现在假设频偏是m(为整数)倍的载波间隔,则:y’(k)=FFT(x(n)ej2πm/N)=Y(k-m),可见,整数倍频偏的影响只是对频域数据进行了循环移位。
本文介绍的移动相关算法主要基于频域最大似然估计理论。现以DVB-T系统为例,每个OFDM符号在频域内都插入了大量的被提升了功率的导频信号,其中连续导频在每个符号内的位置不变。由于时域同步部分对每个符号都进行了粗频率偏移校正,因此,当前后两个符号导频数据相关时,在正确的导频点将得到较大的功率。由于前后符号的数据点不相关,它们的相关值则近似为零。故可将连续的两个符号共扼相乘,然后将导频功率累加:
2.2 小数倍频偏估计
本文采用线性最小平方估计法进行小数倍频偏估计。在OFDM系统的接收端,每个子载波在FFT处理时都可乘上解调因子:
正交频分复用(Orthogonal Frequency DivisionMultiplexing,OFDM)具有高速传输数据、高效的频谱利用率和抗多径的能力。最近几年,OFDM技术已经成功地应用在移动以及固定数据传输中,例如非对称数字用户线路(Asymmetric Digi-tal Subscriber Line,ADSL)、数字视频广播(DVB-T和DVB-H),以及无线局域网(WirelessLAN)等。目前,OFDM已被视为第四代移动通信最具竞争力的传输技术。由于OFDM在频域把信道分成许多正交子信道,各子信道的载波间保持正交,且频谱相互重叠,这样就减小了子信道间的干扰,提高了频谱利用率。所以,OFDM系统对频率偏移非常敏感,很小的频率偏移都可能破坏子载波间的正交性,从而产生载波间干扰(ICI)以造成系统性能的严重下降。因此,在OFDM系统中,频率偏移估计的准确性至关重要。
1 OFDM系统及其同步要求
OFDM系统能有效地对抗信道多径衰落;它通过将串行数据流调制到并行的子载波上,可在很大程度上提高带宽利用率;而在传输的数据流码字中插入循环前缀(CP),则能够有效地消除码间干扰和载波间干扰。图1所示是OFDM系统的简单结构。
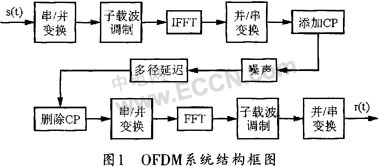

该技术首先对输入信号流进行调制(例如PSK或QAM),以将数据流通过IDFT调制到N个子载波上,然后经过IDFT使每个符号的后L个抽样被复制到符号前端以形成循环前缀,再经过信道传输,并在接收端除去循环前缀,接着将接收到的符号经过DFT变换,这样就能恢复传输信号。在信道上传输的信号可能会受到噪声干扰,这是因为接收端和发送端的频率不匹配,此外,多普勒频移也会产生频率偏移。如不考虑信道衰落的影响,接收符号和发送符号之间的关系如下:

2 频率同步算法
由Jan-Japp提出的最大似然估计(ML)算法具有计算量小、冗余度低、算法实现简单、可同时估计定时和频偏的优点。但该算法的频率估计范围过小,定时估计较为粗糙,不能直接用到实际系统中。由ML算法估计的实际相对频差为:


频偏估计时通常将频率偏移划分成分数部分和整数部分。这里是以子载波间隔作为归一化标准。子载波间隔的整数倍的频偏称为整数部分频偏,剩余的小于一个子载波问隔的频偏称为分数部分频偏。整数频偏经IFFT变换后通常表现成对应子载波标号的偏移,而分数倍频偏则表现为相位的旋转。由于OFDM系统存在大量的提升功率的导频,因此,只要搜索到这些导频就可以得到整数倍频率偏移,而检测导频的相位又可以得到分数倍频偏。估计到的频率误差除了要送到后一级以实时纠正数据的相位外,为了减小载波间干扰,还必须将其前馈到时域进行频率校正,因此频偏的校正示意图可用图2来说明。
2.1 整数倍频偏估计
一般来说,整数倍频率同步的作用是对频率整数倍子载波间隔部分进行估计。没有频偏时的频域信号Y(k)=FFT(y(n))=FFT(x(n)),现在假设频偏是m(为整数)倍的载波间隔,则:y’(k)=FFT(x(n)ej2πm/N)=Y(k-m),可见,整数倍频偏的影响只是对频域数据进行了循环移位。
本文介绍的移动相关算法主要基于频域最大似然估计理论。现以DVB-T系统为例,每个OFDM符号在频域内都插入了大量的被提升了功率的导频信号,其中连续导频在每个符号内的位置不变。由于时域同步部分对每个符号都进行了粗频率偏移校正,因此,当前后两个符号导频数据相关时,在正确的导频点将得到较大的功率。由于前后符号的数据点不相关,它们的相关值则近似为零。故可将连续的两个符号共扼相乘,然后将导频功率累加:
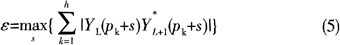
2.2 小数倍频偏估计
本文采用线性最小平方估计法进行小数倍频偏估计。在OFDM系统的接收端,每个子载波在FFT处理时都可乘上解调因子:
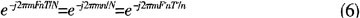


 将整偏校掉后,△f0仅为小数倍
将整偏校掉后,△f0仅为小数倍
仿真 相关文章:
- 一种基于OPNET的小型网络仿真及分析(04-08)
- APOX软件在A+B频段无线网络规划中的应用(06-26)
- 基于GUI的跳频OFDM系统仿真设计(03-03)
- 基于CPLD的RS-232串口通信实现(04-23)
- 2.5 Gbps收发器中1∶2解复用电路的设计(09-17)
- 填补网络 SoC 设计前端与后端验证的差距(09-19)
