开槽波导3次谐波回旋行波放大管非线性理论与数值模拟
本文讨论了开槽圆柱波导的高频场分布,给出了注波互作用自洽非线性理论.在电子作大回旋运动与考虑速度零散的情况下,采用四阶龙格库塔法,对均匀截面开槽波导3次谐波回旋行波放大管注波互作用进行了数值计算,得出一些重要的互作用规律,为回旋行波放大管的进一步研究打下了基础.
关键词:回旋行波放大管;开槽波导;自洽非线性;高次谐波;速度零散
Self-Consistent Nonlinear Theory and Simulation of a Slotted Third-Harmonic Gyro-TWT Amplifier
ZHANG Hong-bin,LI Hong-fu,ZHOU Xiao-lan,WANG Hua-jun,YU Sheng,DU Pin-zhong
(Inst.of High Energy Electronics,UEST of China,Chengdu 610054,China)
Abstract:The distribution of RF field of the slotted cylindrincal wave guide is discussed and the self-consistent nonlinear theory of the beam-wave interaction is presented in this paper.The behavior of the slotted gyrotron travelling-wave amplifier (gyro-TWT) with a uniform section is simulated by a Runge-Kutta algorithm code for a warm beam encircling around the axis of the wave guide.Some important regulations are obtained.This work presents the bases to further studies of the gyro-TWT.
Key words:Gyro-TWT;slotted wave guide;self-consistent nonlinear;high harmonic wave;velocity spread
一、引 言
回旋行波放大管属于毫米波放大器件,它以高功率、高效率、宽频带而著称,在雷达与通讯等领域有着极其重要的应用前景,自七十年代末以来,在理论和实验方面都取得了长足的进展[1~5].
对于基次谐波回旋行波管,在毫米波波段需要很高的直流磁场,因而需要体积较大的超导系统或电磁铁系统来提供直流磁场.采用高次谐波互作用,便可大大降低管子对直流磁场的要求[2,3],使采用永久磁铁成为可能,从而可大大减小管子的体积.由于开槽壁和光滑壁波导中高频场分布存在的差异,开槽波导更有利于注波互作用,对工作电压要求较低,工作效率比光滑壁波导要高,同时与光滑壁波导相比具有很好的模式竞争抑制能力[6].本文以95GHz开槽3次谐波为例,对回旋行波放大管进行了数值模拟,得到了一些重要的互作用规律.
二、高频场模式和特性
图1所示为开槽波导结构以及电子注轨迹横截面图(虚圆表示电注横截面图).设N为开槽波导的槽数,θ0为间隙半张角,a、b分别为波导内外半径,r、φ、z为电子的柱坐标,v⊥为电子的横向速度,φ为动量空间角,即v⊥与x轴夹角.为了方便起见,将波导分为两个区域进行讨论,即:Ⅰ区(0<r<a)和Ⅱ区(a<r<b).由于在回旋行波管中电子注与波的有效互作用场为TE波场,故仅需关心横电波高频场的分布情况[7~9].这里只给出了高频电场分量的表达式,有关高频磁场分量的表达式可进一步能过电磁场分量关系求得.
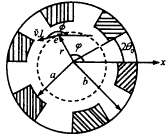
图1 中空外开槽波导及电子注横截面示意图.虚圆为电子注横截面示意图 在Ⅰ区(0<r<a)中
在Ⅱ区(a<r<b)中 Ez=0 (4)
其中
在以上各式中,E0为高频场振幅,Γ为角向谐波数,ΑΓ为角向Γ次谐波项的振幅系数,kc为截止波数,q为开槽序数(q=1,2,…,N),m代表高频场的角向模式(m=0,1,2,…,N-1).AΓ的值以及电路的色散关系可由电磁场在r=a处的边界条件确定.
色散关系为
式(9)表明,只有当空间谐波次数Γ=m+lN时,非零空间谐波项才存在.角向模式决定相邻隙间高频场的相位差,对于每一具体模式,此相位差值为m2π/N.每一角向模式均由无数个角向谐波项组成,其谐波振幅系数由式(9)决定.在所有角向模式中有两个比较重要的模式,即π模式和2π模式,其角向谐波相对强弱分布情况见图2.由图2可知,2π模式的能量主要集中于零次谐波项中,而π模式的能量主要集中于±N/2次谐波项中.因此,π模式较2π模式更适合于高次回旋谐波互作用.如果电子注回旋谐波次数(用S表示)已经设定,那么槽数N的选择应保证最强非零次角向谐波项的次数Г与回旋谐波次数S相等.如,对于π模式,槽数N应等于2S. |
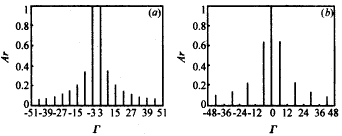
图2 角向谐波振幅对角向谐波数(Γ)的相对分布示意图.(a)π模式(m=N/2,N=6,θ0=15°),(b)2π模式(m=0,N=6,θ0=15°) 当角向模式m和槽深(即a/b的值)确定后,截止波数kc的值可由式(10)通过数值求解方法 |

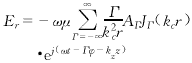 (1)
(1)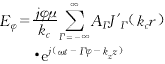 (2)
(2)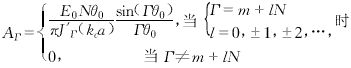 (9)
(9)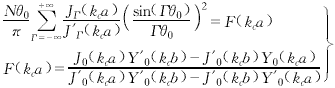 (10)
(10)