一种紧缩结构的基片集成波导双通带滤波器

1、引言

在现代微波无线通信系统中，滤波器和双工器等无源器件有着十分重要的作用。如果采用传统的金属波导、微带线或者共面波导来设计，不是造价昂贵就是很难达到所要求的技术指标。另一方面，随着微波毫米波集成电路的迅速发展，这些传统的微波电路结构已经不能适应现代无线通信对微波元器件小型化、集成化的要求。基片集成波导(Substrate Integrated Waveguide)通过周期性金属通孔实现了的类波导结构，继承了传统波导器件高品质因数和大功率容量等优良特性，被广泛应用于设计各种微波和毫米波器件，同时基片集成波导还具有易于加工、造价低和容易集成的优点。

为了产生传输零点，目前很多滤波器的设计采用交叉耦合的形式，极点提取技术与其相比，优势主要体现在衰减极点频率的可控性，简化了滤波器的结构，降低了复杂结构带来的敏感性，而且降低了滤波器调谐和加工的难度。本文利用极点提取技术和耦合矩阵方法，提出了一种新型结构的基片集成波导双通带滤波器。该滤波器采用单一谐振腔提取衰减极点，利用一个滤波器结构实现双通带响应，仿真结果显示两个通带形成很高的隔离度，通带内回波损耗很小。该滤波器谐振腔采用三角形SIW谐振腔，整个滤波器构成一个六边形，结构紧凑，有效的减小了滤波器的尺寸。

2、等效电路分析

以六腔滤波器为例，等效电路如图1所示，第二腔和第六腔作为吸收回路提取衰减极点，衰减极点的位置就是第二、六腔谐振的位置，因此衰减极点的位置可任意确定，这使极点提取技术的应用有了很大的灵活性，利用一个滤波器结构，就可以实现两种不同响应类型的滤波器：其一，衰减极点在通带外，可以设计带外有传输零点的带通滤波器，以增强带外抑制;其二，衰减极点在通带内部，可以设计双通带滤波器。本文提出的滤波器第一、三、四、五腔构成一个带通滤波器结构，而第二、六腔提取的衰减极点在通带内部，由此形成一个双通带结构。

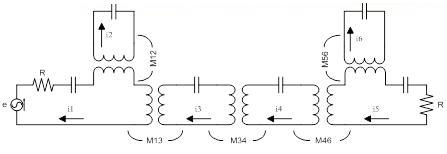
图1、双通带滤波器等效电路

为了验证该设计方法的可行性，设计了一个双通带滤波器。设计指标为：两个通带为9.6-9.85GHz和10.15-10.4GHz,通带插损小于0.5dB，回波损耗小于-15dB，两通带隔离小于-20dB。原理电路如图1所示。由文献[7]给出的方法计算出各腔之间的耦合系数和外部Q值，数据如下。在microwave office中进行电路级仿真，结果如图2所示，得到了预想中的波形，验证了该设计方法的可行性。

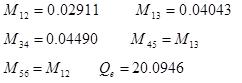
3、滤波器设计

3.1、三角形SIW腔体的研究

与长方形SIW腔体比较，等边三角形SIW腔体具有其自身的特点与性质。本文提出的滤波器与中介绍的滤波器同样由六个谐振腔构成，与中采用长方形SIW腔体不同的是，本文所介绍的滤波器采用等边三角形SIW腔体，由于这一变化，占空比明显减小，有效的利用了空间，实现了滤波器的小型化。

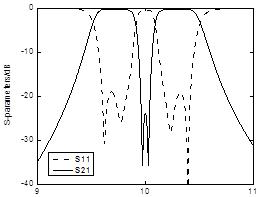
图2、电路级仿真结果

等边三角形SIW腔体磁场分布如图3所示，磁场是环绕三角形中心的封闭曲线。文献[9]给出了计算正方形和圆形SIW腔体主模谐振频率的公式，而等边三角形SIW腔体主模频率表可由式(1)得到：

(1)

公式(1)中，F为三角形谐振腔主模谐振频率，c为真空中的光速，为介质相对介电常数，L为等边三角形边长。

图3、等边三角形SIW腔体磁场分布

为验证计算公式，我们选取一组不同边长的等边三角形SIW腔体进行试验。表1为应用公式(1)求得的频率与应用CST MICROWAVE STUDIO仿真得到的频率的比较。结果显示，公式计算得到的频率与仿真得到的频率吻合较好，验证了等边三角形SIW腔体主模频率计算公式的正确性。

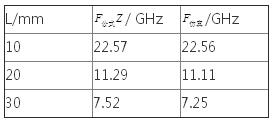
3.2、滤波器仿真与测试结果

图4、滤波器结构图

表2、滤波器物理结构尺寸(单位：mm)

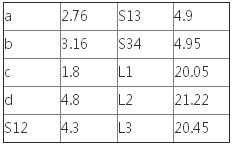
为了验证设计方法的有效性，设计了一个x波段基片集成波导双通带滤波器。采用相对介电常数为2.65和厚度1mm的介质板，金属通孔直径0.5mm，孔间距1mm，图4为滤波器结构图。其中a为50欧姆导带宽度，b、c、d决定了滤波器的外部Q值，L1、L2、L3分别为第一、二、三腔的边长，决定各腔体的谐振频率，S12、S13、S34分别为相邻2腔耦合孔的大小，决定相邻两腔耦合的强弱。最后经过CST MICROWAVE STUDIO仿真优化后，可得到滤波器的物理尺寸，如表2所示，滤波器结构左右对称。仿真结果如图5所示。

图5、CST仿真结果

4、结论

本文提出了一种新型的基片集成波导双通带滤波器，并给出了具体的设计步骤。着重研究了等边三角形SIW腔体的特性，给出了等边三角形SIW腔体主模频率计算公式，经过仿真验证计算结果较为准确。仿真了一个基于三角形SIW腔体的双通带滤波器，该滤波器两个通带之间有很高的隔离度，带内插损较小，仿真结果良好。这种滤波器结构紧