开槽波导3次谐波回旋行波放大管非线性理论与数值模拟
| 内半径 | 1.024mm |
| 外半径 | 1.465mm |
| 电路长度 | 87.9mm |
| 注电压 | 60kV |
| 注电流 | 6A |
| α | 1.3 |
| 直流磁场 | 11.674kG |
| 高频场模式 | π |
| 谐波次数 | 3 |
| 工作频率 | 95.08GHz |
| 模拟结果 | |
| 饱和效率 | 22.8% |
| 饱和输出功率 | 82kW |
| 饱和增益 | 36.15dB |
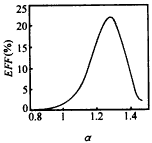
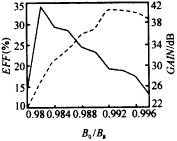
图3 效率与电子注速度比值α的关系(s=3,πmode,I=6A,V=60kV,ω/ωc=1.032, 图4所示为饱和效率、饱和增益与B0/Bg值之间的关系,虚线为饱和增益曲线.图中γz为纵向速度分量的相对论因子.图示表明,一方面,降低B0/Bg值,有助于提高饱和互作用效率,但B0/Bg值不能太低,否则失谐加重,注波互作用难以达到同步,饱和效率便会迅速降低;另一方面,增加B0/Bg的值却有利于提高饱和增益.总的来说,磁场失谐率的选择应在效率和增益之间作优化折衷.
图4 饱和效率及增益与B0/Bg值的关系(s=3,π mode,I=6A,V=60kV,ω/ωc=γz, 图5所示电流分别为3A、6A和9A情况下(a)饱和效率、(b)饱和增益随频率变化的关系.可以看出饱和效率、饱和增益以及饱和 |
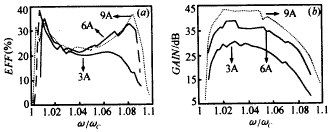
图5 不同电流下,(a)饱和效率(b)饱和增益随频率变化的关系(s=3,π mode,V=60kV,α=1.3,B0/Bg=0.99) 图6所示为几个不同磁场失谐率下饱和增益以及饱和效率随频率变化的关系.由图可见,磁场失谐率对饱和增益、饱和效率及饱和带宽都有较大影响,B0/Bg值的提高有利于饱和增益及饱和带宽的提高,但饱和效率却有所降低.在图示条件下,当B0/Bg值从0.983增大到0.998时,饱和带宽从4.8%增大到9.3%. |

图6 不同磁场失谐率下,(a)饱和增益及(b)饱和效率随频率变化的关系(s=3,π mode,I=6A,V=60kV,α=1.3) 图7为在不同磁场失谐率下饱和效率随谐波次数的变化关系.由图表明,饱和效率随谐波次数的增大而降低,B0/Bg值越低,谐波次数对饱和效率的影响越大. |
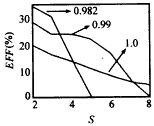
图7 饱和效率随谐波次数的变化关系(π mode,I=6A,V=60kV,α=1.3,ω/ωc=γz,rL/a=0.7) 图8所示为不同谐波次数下饱和效率随频率的变化关系.图示表明 |

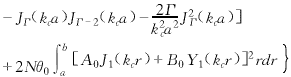 (14)
(14)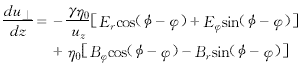 (15)
(15)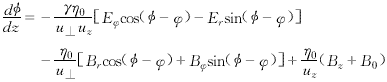 (17)
(17)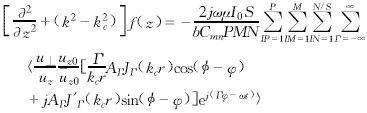 (18)
(18)