运算放大器电路设计技巧1：试试这样搞定运放在补偿器动态响应

步骤。

 

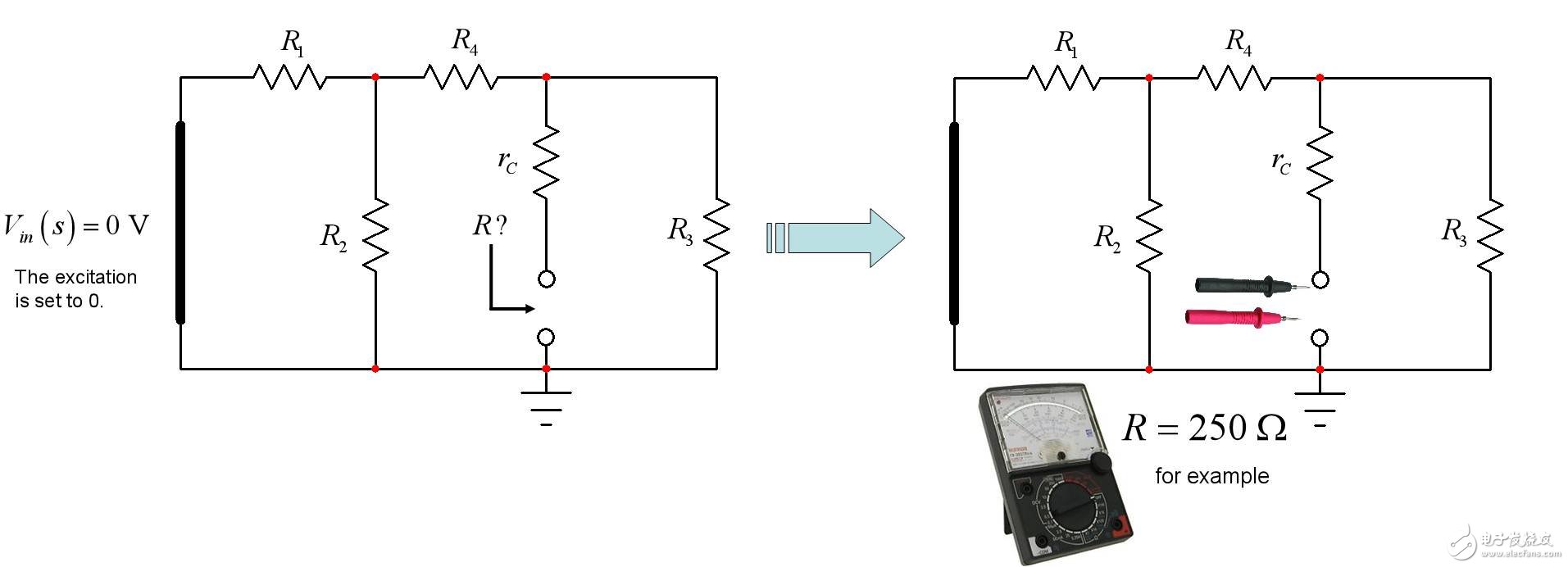
The excitation is set to 0：励磁设为0

For example：例如

图4：在 0V 源换为短路后，您确定电容器端的电阻。

 

如果您按图4进行练习，您"看到" R₁ 与 R₂ 并联后与与 R₄ 串联，所有这些与 R₃ 并联后与 r_C 串联。该电路的时间常数只通过 R 和 C₁ 即可计算得出：

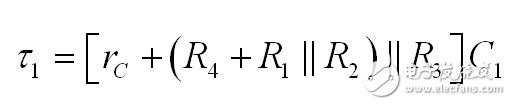
（2）

 

我们可证明，一个第一阶系统的极点是其时间常数的倒数。因此：

 

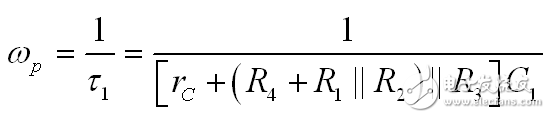
（3）

 

现在， s = 0 时这个电路的准静态增益是多少？在直流条件下，电感器短路，电容器开路。把这个概念应用于图3的电路，绘制如图5所示。您想象在 R ₄ 前切断连接，会看到一个含 R₁ 和 R₂ 的电阻分压器。R₂ 上的戴维宁(Thévenin)电压为：

 

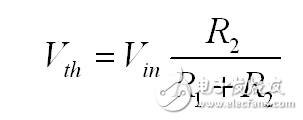
（4）

 

输出电阻 R_th  是 R₁ 与 R₂ 并联的值。因此完整的传递函数涉及到与 R_th  串联的 R₄ 和加载的 R₃ 所构成的电阻分压器。r_C 是断开的，由于电容 C₁ 在这直流分析中被移除。因此可写：

 

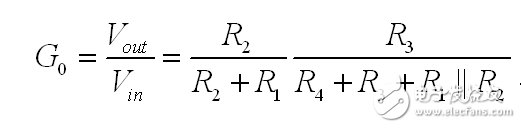
（5）

 

您断开直流电路中的电容器，计算这个简单的电阻排列的传递函数。

 

基本就是这些了，我们正错过零点。我们如何知道是否到了零点？嗯，这是个有用的技巧：在你的头脑中考虑图3的电路，短路电容 C₁ 。现在，假设您激励具有短路电容器的电路。您能够基于示波器观察 V_out 的响应吗？当然， r_C 短路 R₃ ，尽管振幅可能低，输入信号仍会传播并有响应。如果这个练习的答案是"是的，尽管 C₁ 短路，但仍然有响应"那么有与 C₁ 有关的零点。如果您处理含一个电感 L₁ 的电路，然后进行同样的练习，但采用电感开路。如果在这模式仍有响应，那么有与 L₁ 有关的零点。

 

我们在序言中说，零点通过阻断激励信号的传播而在电路中表现出来，并产生输出为空。如果我们考虑一个变形电路–其中 C₁ 被

1/sC₁ 代替–如图6所示，当励磁偏移网络，有什么特定的条件意味着响应为空？有一个空响应只意味在 R₃ 循环的电流为0。如果电阻没有电流，没有电压施加和 V_out 是 0 V，这不是短路，而是虚拟的接地。

 

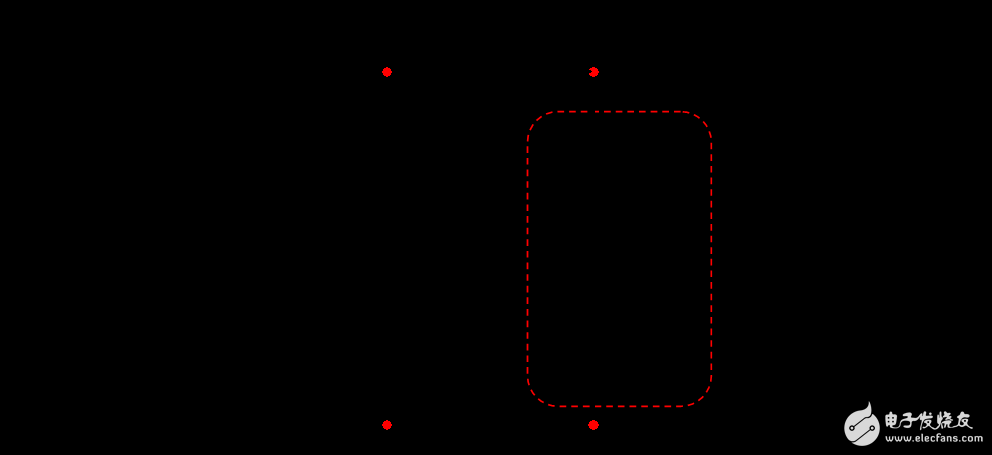 图6：在这变形电路中，当 r_C 和 C₁ 串联转化为短路，响应消失。

 

如果 R₃ 没有电流，那么 r_C  和 1/sC₁ 串联创建一个转换的短路：

 

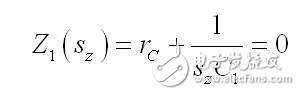
（6）

 

根 s_z 是我们需要的零点位置：

 

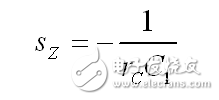
（7）

从而有：

 

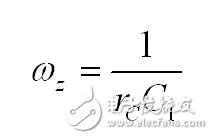
（8）

 

现在，我们可以组合所有这些结果，形成以图3电路为特征的最终的传递函数：

 

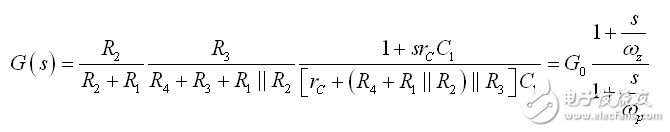
（9）

 

这就是所谓的低熵表达式，您可立即识别增益、极点和零点。高熵表达式将在考虑阻抗分压器时通过施加大规模外力到原来的电路来获得，例如：

 

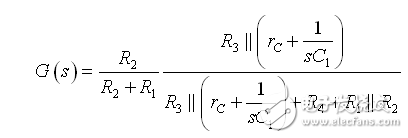
（10）

 

不只您可能在推导表达式时犯错误--我也会！但是将结果格式化到像（9）这样需要更多的精力。此外，请注意，在写（9）时我们没有写一行代数。如果我们后来发现一个错误，那么易于回到一个单独的图纸并单独修复它。（9）的校正将是容易的。现在尝试在（10）进行相同的修正，您可能会从头开始。您检查一下，在 Mathcad® 表绘制的表达式（9）和（10）的频率响应是相同的，如图7所示。

 

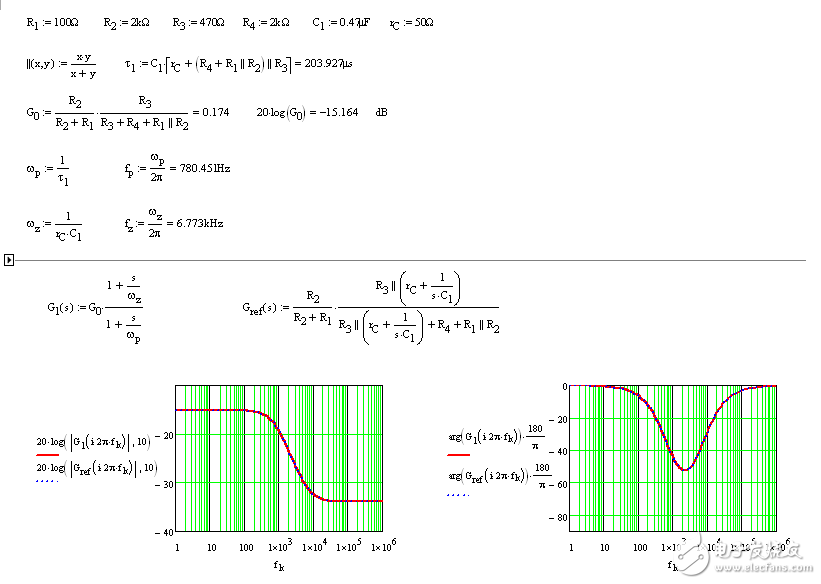
图7：快速 Mathcad® 告诉您用 FACTs 推导出的表达式是否与由原表达式返回的响应相匹配。

 

FACTs 的简介意在说明在简单和更复杂的电路上使用它们是多么轻松和高效。通过将一个复杂的体系结构分解为简单的单独的电路，您可以很快地编写传递函数，有时只通过检查，正如我们所做的那样。既然我们已介绍了工具，让我们把它应用到我们的 type 2 补偿器。

 

FACTs 应用于 Type-2 补偿器

为高效地运用 FACTs 到图2的电路，我们开始于计算储能元件： C₁ 和 C₂ 。考虑到它们的独立状态可变—如它们不是串联的或并行的--这是个二阶系统。考虑非零准静态增益，这样的系统可以表示为以下形式：

 

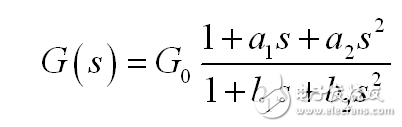
（11）

 

对于二阶系统，我们可以证明分母遵循下列公式：

 

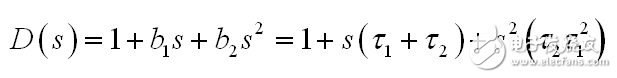
（12）

 

系数 s 仅仅是确定零点激励的时间常数之和。S² 系数稍微复杂，因为它引入了一个新的符号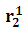：。此符号意味着您"看到"的 C₂ 终端的阻抗，而 C₁ 由短路取代。乍一看有点难以理解，但没有不可逾越的，我们用几句话解释就会明白。

 

按照求解图3电路的途径，我们可研究 s = 0 的系统，如图8所示。在分析的过