3种机器学习算法解读

个方面，以及1973 - 1974年生产的32辆汽车的性能。

　　使用R，我们将根据V/S和Miles/（US）加仑的测量值，预测自动变速器（am = 0）或手动（am = 1）汽车的概率。

　　am = g（a * mpg + b* vs +c）：

　　结果如下图所示，其中黑点代表数据集的初始点，蓝色线代表a = 0.5359，b = - 2.7957，c = - 9.9183的拟合逻辑回归线。

　　正如前面所提到的，我们可以观察到由于回归线的形式，logisTIc回归输出值只在范围［0，1］中。

　　对于任何以V/S和Miles/（US）加仑为标准的新车，我们现在可以预测这辆车自动变速器的概率。

　　决策树

　　决策树是我们将要研究的第二种机器学习算法。决策树最终分裂成了回归和分类树，因此可以用于有监督学习问题。

　　诚然，决策树是最直观的算法之一，它们可以模仿人们在大多数情况下的决定方式。他们所做的基本上就是绘制出所有可能路径的"地图"，并在每种情况下画出相应的结果。

　　图形表示将有助于更好地理解我们正在讨论的内容。

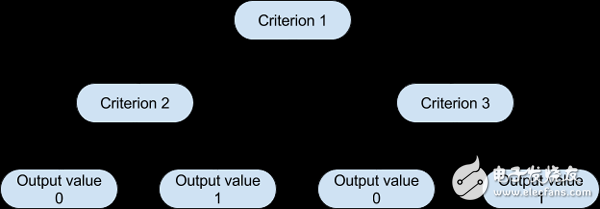
　　基于这样一棵树，算法可以根据相应的标准值决定在每个步骤中遵循哪条路径。算法选择分割标准的方式和每个级别的相应阈值，取决于候选变量对目标变量的信息量，以及哪个设置最小化了所产生的预测错误。

　　这里还有一个例子！

　　这一次讨论的数据集是readingSkills。它包括了学生的考试成绩和分数。

　　我们将基于多种指标把学生分为母语为英语的人（naTIveSpeaker = 1）或外国人（naTIveSpeaker = 0），包括他们在测试中的得分，他们的鞋码，以及他们的年龄。

　　对于R中的实现，我们首先需要安装party包。

　　我们可以看到，使用的第一个分裂标准是分数，因为它在预测目标变量时非常重要，而鞋子的大小并没有被考虑在内，因为它没有提供任何关于语言的有用信息。

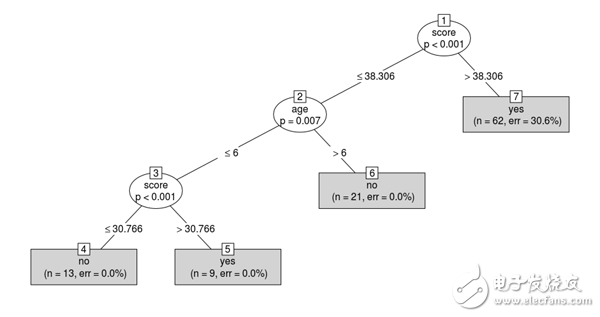
　　现在，如果我们有了一个新学生，知道他们的年龄和分数，我们就可以预测他们是不是一个以英语为母语的人！

　　聚类算法

　　到目前为止，我们只讨论了一些关于有监督学习的问题。现在，我们继续研究聚类算法，而它则是无监督学习方法的子集。

　　所以，只是稍微修改了一点…

　　对于集群，如果有一些初始数据进行支配，我们想要形成一个组，这样一些组的数据点是相似的，并且不同于其他组的数据点。

　　我们将要学习的算法叫做k-means，k表示产生的簇的数量，这是最流行的聚类方法之一。

　　还记得我们之前用过的Iris数据集吗？我们将再次使用它。

　　为了研究，我们用他们的花瓣测量方法绘制了数据集的所有数据点，如下图所示：

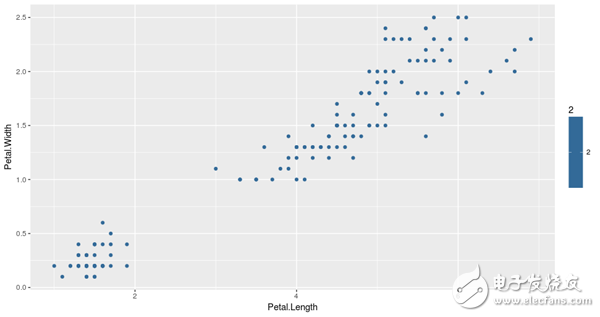
　　基于花瓣的度量值，我们将使用3-means clustering方法将数据点聚集成3组。

　　那么3-means，或者说是k-means算法是如何工作的呢？整个过程可以用几个简单的步骤来概括：

　　初始化步骤：对于k = 3簇，算法随机选取3个点作为每个集群的中心点。

　　集群分配步骤：算法通过其余的数据点，并将每个数据点分配给最近的集群。

　　Centroid移动步骤：在集群分配之后，每个集群的中心点移动到属于集群的所有点的平均值。

　　步骤2和步骤3重复多次，直到对集群分配没有更改。R中k-means算法的实现很简单，可以用以下代码实现：

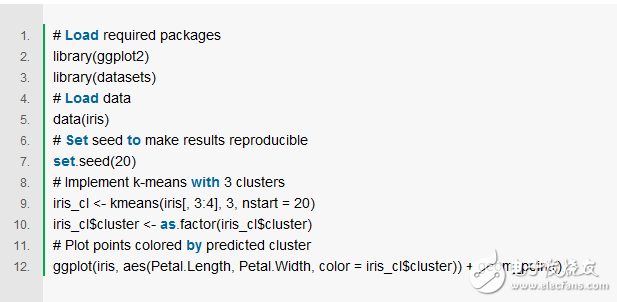
　　从结果中可以看出，该算法将数据分成三组，分别用三种不同的颜色表示。我们也可以观察到这些簇是根据花瓣的大小形成的。更具体地说，红色表示花瓣小的花，绿色表示花瓣相对较大的蝴蝶花，而蓝色则表示中等大小的花瓣。

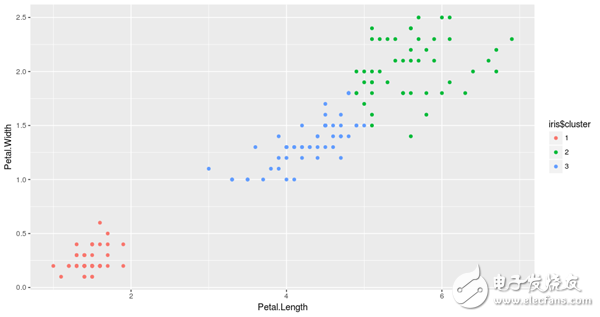
　　值得注意的是，在任何聚类中，对形成群体的解释都需要在该领域有一些专家知识。在我们的例子中，如果你不是一个植物学家，你可能不会意识到k - means所做的是把iris聚集到他们不同的类型，例如Setosa，Versicolor和Virginica，而没有任何关于它们的知识！

　　因此，如果我们再次绘制数据，这个时间被它们的物种着色，我们将看到集群中的相似性。

　　总结

　　我们从一开始就走了很长一段路。我们讨论了回归（线性和逻辑）和决策树，最后讨论了k - means集群。我们还在R中实现了一些简单但强大的方法。

　　那么，每种算法的优点是什么呢？在现实生活中，你应该选择哪一个？

　　首先，所呈现的方法并不是一些不适用的算法——它们在世界各地的生产系统中被广泛使用，因此需要根据不同的任务进行选择，选择恰当的话可以变得相当强大。

　　其次，为了回答上述问题，你必须清楚你所说的优点究竟是什么意思，因为每种方法在不同环境中展现出来的优点是不同的，例如解释性、稳健性、计算时间等。