3种机器学习算法解读

　　在下面的文章中，我们将讨论决策树、聚类算法和回归，指出它们之间的差异，并找出如何根据不同的案例选择最合适的模型。

　　有监督学习 VS 无监督学习

　　理解机器学习的基础就是如何对有监督学习和无监督学习这两个大类进行分类的问题，因为机器学习问题中的任何一个问题最终都是这两个大类中的某一个。

　　在有监督学习的情况下，我们有数据集，某些算法会将这些数据集作为输入。前提是我们已经知道正确的输出格式应该是什么样子（假设输入和输出之间存在某种关系）。

　　稍后我们看到的回归和分类问题都是属于这一类。

　　另一方面，无监督学习适用于我们不确定或者不知道正确的输出应该是什么样子的情况。事实上，我们需要根据数据推导出正确的结构应该是什么样。聚类问题是该类的主要代表。

　　为了使上述分类更加清晰，我将列举一些现实世界的问题，并尝试对它们进行相应的分类。

　　实例1

　　假设你在经营一家房地产公司。考虑到新房子的特点，你想基于之前记录的其他房子的销售情况，从而预测这间房屋的销售价格应该在什么价位。输入的数据集包含多个房子的特征，比如浴室的数量和大小，而你想要预测的变量，通常称为目标变量，在本例子中也就是价格。因为已经知道了数据集中房子的出售价格，因此这是一个有监督学习的问题，说的更具体一点，这是一个关于回归的问题。

　　实例2

　　假设你做了一项实验，根据某些物理测量结果以及遗传因素，来推断某人是否会发展成为近视眼。在这种情况下，输入的数据集是由人体医学特征组成的，目标变量是双重的：1表示那些可能发展近视的人，0表示没有成为近视眼的人。由于已经提前知道了参与实验者的目标变量的值（即你已经知道如果他们是否是近视），这又是一个有监督学习的问题——更具体地说，这是一个分类的问题。

　　实例3

　　假设你负责的公司有很多的客户。根据他们最近与公司的互动结果，最近购买的产品，以及他们的人口统计资料，你想要把相似的客户组成一个群体，以不同的方式来对待他们——比如给他们提供独家折扣券。在这种情况下，将会使用上面提到的某些特性作为算法的输入，而算法将决定应该客户群的数量或类型。这是无监督学习最典型的一个例子，因为我们事先根本就不知道输出结果应该是怎样的。

　　话虽如此，现在是实现我的承诺的时候了，来介绍一些更具体的算法……

　　回归

　　首先，回归不是单一的有监督学习的技术，而是许多技术所属的整个类别。

　　回归的主要思想是给定一些输入变量，我们想要预测目标变量的值是什么样的。在回归的情况下，目标变量是连续的——这意味着它可以在指定范围内取任意的值。另一方面，输入变量既可以是离散的，也可以是连续的。

　　在回归技术中，最广为人知的就是线性回归和逻辑回归了。让我们仔细研究研究。

　　线性回归

　　在线性回归中，我们试图建立输入变量与目标变量之间的关系，这种关系是由一条直线表示的，通常称为回归线。

　　例如，假设我们有两个输入变量X1和X2以及一个目标变量Y，这种关系可以用数学形式表示：

　　Y = a * X1 + b*X2 +c

　　假设已经提供了X1和X2的值，我们的目标是对a、b、c三个参数进行调整，从而使Y尽可能接近实际值。

　　花点时间讲个例子吧！

　　假设我们已经有了Iris数据集，它已经包含了不同类型的花朵的萼片和花瓣的大小数据，例如：Setosa，Versicolor和Virginica。

　　使用R软件，假设已经提供了花瓣的宽度和长度，我们需要实现一个线性回归来预测萼片的长度。

　　在数学上，我们将通过如下关系是获取a、b的值：

　　SepalLength = a * PetalWidth + b* PetalLength +c

　　相应的代码如下：

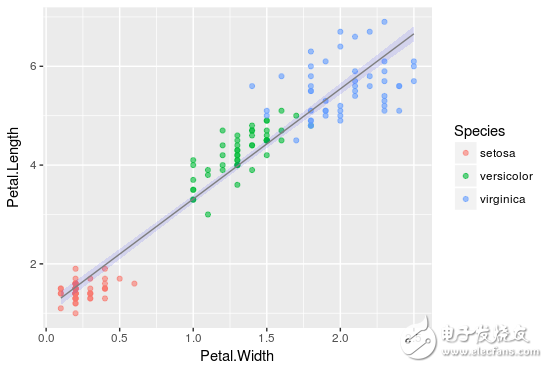
　　线性回归的结果如下图所示，黑点表示初始数据点在蓝线拟合回归直线，于是便有了估算结果，a= -0.31955，b = 0.54178，和c = 4.19058，这个结果可能最接近实际情况，即花萼的长度。

　　从现在开始，通过将花瓣长度和花瓣宽度的值应用到定义的线性关系中来，新出现的数据点我们也可以预测它的长度了。

　　逻辑回归

　　这里的主要思想和线性回归完全一样。最大的不同就是回归线不再是直的的。

　　相反，我们试图建立的数学关系是类似于以下形式：

　　Y=g（a*X1+b*X2）

　　这里的g（）就是逻辑函数。

　　由于logisTIc函数的性质，Y是连续的，在［0，1］范围内，可以理解为事件发生的概率。

　　我知道你喜欢例子，所以我再给你看一个！

这次，我们将对mtcars数据集进行实验，该数据集包括燃料消耗和汽车设计的10