电阻电路的等效变换详细解析

　　 等效变换
         等效是电路分析中一种很重要的思维方法。根据电路等效的概念，可将一个结构较复杂的电路变换成结构简单的电路，使电路的分析简化。

　　 等效的概念

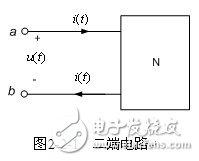
　　【二端电路（一端口电路）】 两端电路具有以下特点：只有两个端钮（a，b）与外部电路相连；进出端钮的电流相同，如图2-2-1所示。二端电路元件，例如电阻元件、独立源、电容元件、电感元件，可视为二端电路的特例，也称二端元件。二端电路也称为一端口电路，一端口电路端口电压、电流的关系称为一端口网络的端口特性或端口VCR。

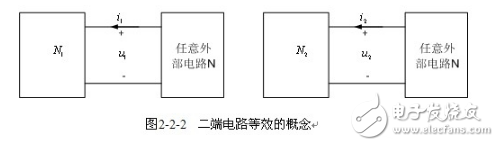
　　【等效电路】 两个二端电路，，如图2-2-2所示，无论两者内部的结构如何不同，只要它们的端口电压、电流的关系（ VCR）相同，则称和是等效的。两个内部结构不同的电路等效的唯一标准是两者对应端口处的VCR完全一致，即它们对同一任意外部电路的效果完全相同。等效是对外部电路而言的，对于互相等效的两个电路，，内部的工作状态是不等效的。等效具有传递性，如果二端电路和等效，二端电路又与等效，则必有与等效。

　　电阻的串联与并联等效变换

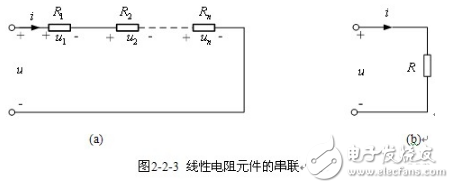
　　【电阻元件的串联】图2-2-3（a）中，由KVL得

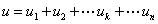
　　且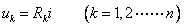 　

　　由KVL得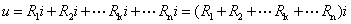

　　令

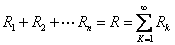
　　则

　　根据上式可以构造一个相应电路如图2-2-3（b）所示，所以图（a）和（b）是等效的，等效电阻等于各串联电阻元件电阻之和。

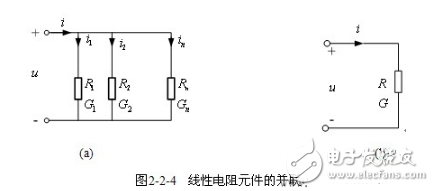
　　【电阻元件的并联】图2-2-4（a）中，由KCL得

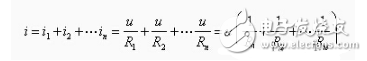
　　令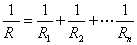

　　用等效电导表示为

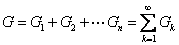
　　星形电阻网络与三角形电阻网络的等效变换

　　由线性电阻元件混联构成的网络，其最简等效电路为线性电阻。但是并非所有由线性电阻元件混联构成的网络都能通过串、并联化简为线性电阻。本小节介绍"平衡电桥"和"星形-三角形"互换两种化简方法。通过这两种方法，在结合电阻元件的串联、并联化简，可实现任何由线性电阻混联构成的网络的等效化简。

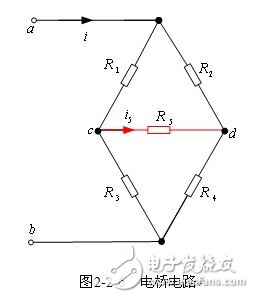
　　【平衡电桥】图2-2-6所示由5个线性电阻（为必要条件）构成的桥式电路中，当或（由于为线性电阻，该两个条件必是同时成立的）时，称此桥式电路为平衡电桥。由平衡电桥电路特点可得到平衡电桥的两种等效电路。由得到图2-2-6所示等效电路；由得到图2-2-6所示等效电路。

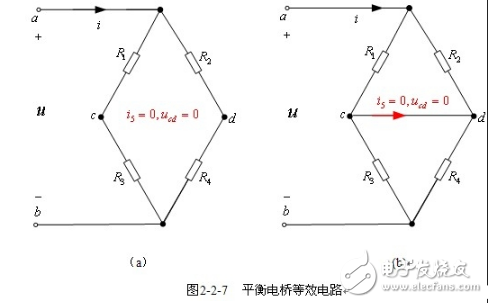
　　【电桥平衡条件】在图2-2-7（a）所示电路中，有

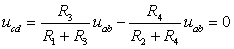
　　在电路2-2-7（b）中 ，有

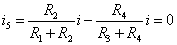
　　由以上两式均可以推出电桥平衡的条件，为

　　【星形—三角形互换】 当电桥不满足平衡条件时，必须采用星形（Y形）与三角形（△形）互换才能将电桥电路化成线性电阻。

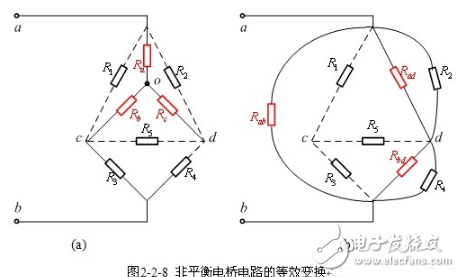
　　如果可将图2-2-6中以节电a，c，d为顶点的三角形电阻，和等效变换成图2-2-8（a）中以新节点o为中心的星形连接电阻，和；或者将图2-2-6中，以c为中心的Y形连接电阻，和等效变换成图2-2-8（b）中以节点a，b，d为顶点的△形连接电阻，和。这样各电阻之间连接关系成为串联和并联关系了。也可以选择△cbd变成Y形，或选择以d为顶点的Y形变为△形。

　　【星形—三角形互换条件】根据前面等效的概念，分别求出这两种电路端钮处的电压-电流关系，让两者相同，即可获得等效条件。

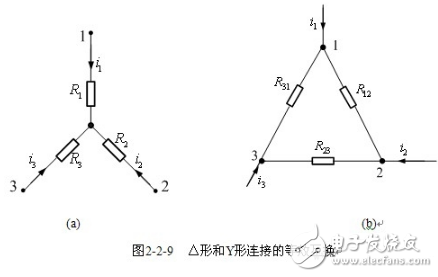
　　在△形电路中，有

　　求解得△形电路中的电压-电流关系

　　而Y形电路中的电压-电流关系为

　　两种电路等效，则端钮处的电压-电流关系应相同。比较△形电路和Y形电路的电压-电流关系，可得△形电路等效变换成Y形电路的条件为

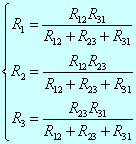　　 （△→Y）

　　同理可得Y形电路等效变换成△形电路的条件为

　　 （Y→△）

　　【例2-2-1】 求图2-2-10（a）所示电路的电流I。

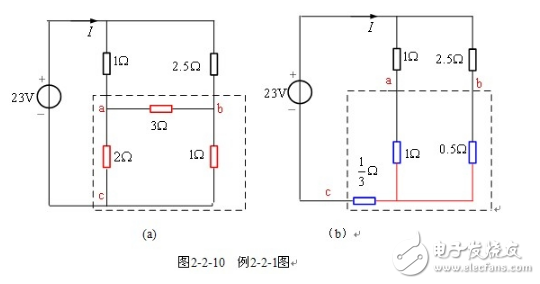
　　将图2-2-10（a）中，，所构成的三角形电路按等效变换为（b）所示电路。则

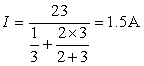
　　4、实际电源的两种模型及其等效变换

　　独立电源是可以用来描述实际电源的电路元件。以下讨论实际直流电源的电路模型。

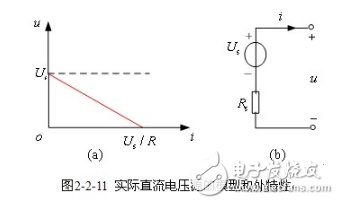
　　【实际直流电压源模型（戴维宁模型）】 一个实际直流电压源的端电压并不是恒定不变的，而是随着输出电流的增加而下降。实际直流电压源外部特性可用图2-2-11（a）所示曲线描述。根据曲线的形状可用独立电压源和线性电阻元件串联的模型来等效，图2-2-11（b）为该实际电源的电路模型，称为戴维宁模型。模型特性方程为

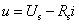
　　当实际电压源内阻很小时，特性曲线趋于与i轴平行，当时，特性曲线与i轴平行，成为理想电压源。

【实际直流电流源模型（诺顿模型）】 一个实际直流电流源，其电流并不是恒定不变的，而是随着端电压的增大而下降。实际直流电流源外部特性可用图2-2-12（a）所示曲线描述，并用图2-2-12（b）所示电路模型来等效，称为诺顿模型，电路模