基础四臂电桥的基本原理和平衡条件

　 四臂电桥的基本原理和平衡条件

　　交流经典电桥中，四臂电桥是最基本的电桥线路，它是对比直流四臂电桥（通常称为单电桥或惠斯登电桥）的结构而发展出来的。为了较好地理解交流四臂电桥的基本原理，现将交流四臂电桥和直流四臂电桥的某些异同点作一简单的比较。两种四臂电桥的电路及各支路元件符号分别表示在图2-3中。

　　两种电桥的相同点有：第一，电路的基本结构形式相同。除了一个电源，一个指零仪支路之外，都有四个桥臂和四个顶点。从电路观点来看，它们都具有六条支路、三个网孔、四个节点。因此当应用电路的一些基本原理去建立方程组时所得到的方程组的形式也将是相同的。第二，这两种电桥，当指零仪指零时，它们实质上都是反映两对相邻桥臂上电压降比值的等量关系。因此电桥的平衡将不受电源电压波动的影响。

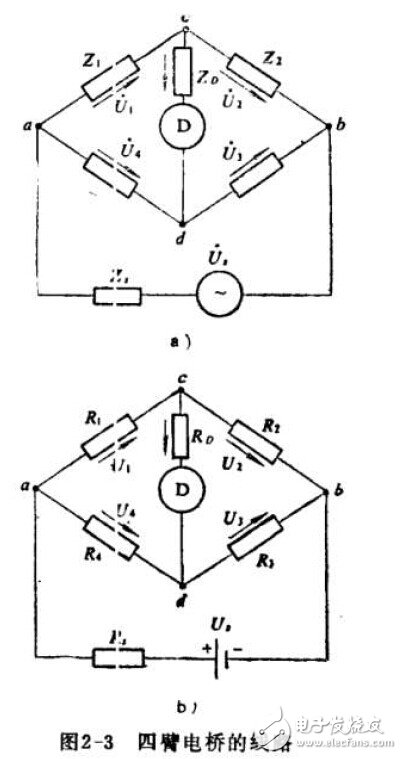
　　两种电桥的不同点可以从下列两方面来说明。第一，各支路元件的性质不同。交流电桥除了需要用交流电源代替直流电源供电之外，并需以某种合适的交流指零仪（报动检流计、耳机、示波器等）代替直流磁电系检流计。另外交流电桥各桥臂一般具有阻抗性质（由电阻、电感和电容元件单独或进行简单的串并联方式所组成），而直流电桥的桥臂只具有电阻性，第二，由于交流电桥的桥臂是阻抗，因此不能像直流电桥那样，只是要求桥臂上的电压降数值进行平衡，而必须同时对桥臂上电压降的相位角进行平衡。换言之，不仅在桥臂间电压的数量关系要满足平衡条件，而且相位角之间也要求满足平衡条件。为此，在桥臂中必须有不少于两个可调参数。

　　交流四臂电桥的基本原理和平衡条件可叙述如下。电桥通常是用正弦交流电源供电，所以我们可以应用相量分析法来描绘桥路的性能。图2-3（ a）中正弦电源的电压相量为Us，四个桥臂阻抗分别用Z1.Z2.Z3和Z4，表示，D为指零仪。一般情况下电源支路和指零仪支路都可能存在着阻抗，它们可分别用Zs和Zd来表示。

　　为了说明电桥的基本原理，可以运用电路理论的某种分析方法来列方程。在列方程之前，有必要重复说明电桥平衡的定义。众所周知，当电桥平衡时，图2-3中的c和d两电桥顶点是等电位的，即该支路两端的电压降为零，也就是指零仪支路中将没有电流流过（即Id=0）。

　　电桥原理和平衡条件的分析方法很多，为简明起见，我们选用桥臂电压降平衡的方法来分析。根据指零仪支路两端等电位的条件，桥臂阻抗Z1上的电压降与阻抗Z4上的电压降应相等，Z2上的电压降与Z3上的电压降相等。即U1=U4，U2=U3。因此，ID为零。由分压公式可得：

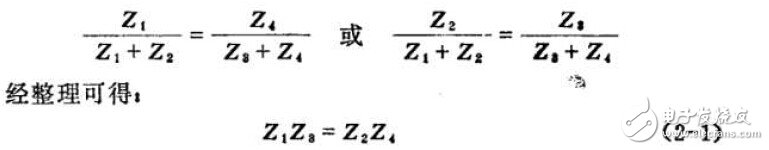
　　对于其体电桥线路，将实际阻坑参数代入式中就可找出各参数间的相互关系。式（2-1）是由基本原理推导而来的平衡条件。此复数方式可用直角坐标形式或指数形式来表示。两种形式分别为：

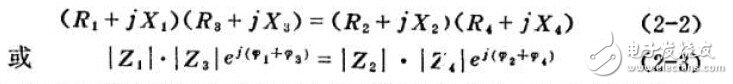
　　式（2-2）的求解是将方程两边实数部分和虚数部分分别相等。即

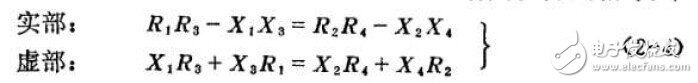
　　这就是四臂电桥平衡时电阻和电抗之问必须满足的条件。从这里还可看到，当所有的电抗均为零值的特殊情况下，平衡条件就变为交流电阻电桥的平衡条件，这与直流单电桥的平衡条件（R1R3 =R2R4）是相同的（可参阅图2-3，）。上述直角坐标形式的平衡条件在电路参数的测量中是非常有用的。

　　式（（2-3）的指数形式（或称极坐标形式）方程可写成：

　　这是四臂电桥平衡条件的另一种形式。显然，要使电桥平衡，不仅电桥两组相对桥臂阻抗的幅值的乘积应该相等，而且其相应的阻抗角之和也应该相等。如果桥臂的幅值之问能满足上述关系，而辐角条件不能满足的话，则仍然不可能使电桥达到平衡。当四个桥臂均为电阻时，各桥臂相应的阻抗角（辐角）为零，此时平衡条件方程式（2-4）或式（2-5）就变为一个，即R1R3=R2R4指数形式的平衡条件对于设计电桥或组合自接电桥是十分有用的。从使用的角度来看，这种形式可以非常直观地指导平衡调节

　　过程四臂电桥各桥臂有时是简单地串联或并联。对于并联方式用导纳代替阻抗将会更加方便。当方程式Z1Z3 =Z2Z4用导纳形式表示时，可以写成

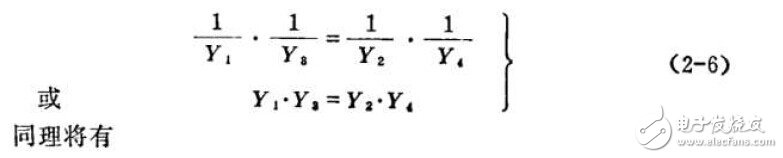
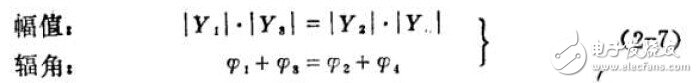
　　这里辐角仍然是原来的阻抗角，因为对于同一个元件上的导纳角数值上等于阻抗角，仅仅差一个负号，这些负号将在方程两边消去，因此对辐角平衡条件言，式（2-7）与（2-5）是一致的。

对于不同参数的桥臂，从以上这些基本平衡条件出发，可以得到各种具体四臂电桥的平衡条件。推导出各种电桥平衡条件的目的是为了寻求未知参数和已知参数之间的关系，以便于电桥根据桥臂已知读数直接或间接地求得未知的电路参数。例如，某种类型的四臂电桥（欧文电桥）如图2-4所示，若R1和L