电路设计宝典：轻松开启PCB设计之门

　　一、PCB Layout中的走线策略

　　布线（Layout）是PCB设计工程师最基本的工作技能之一。走线的好坏将直接影响到整个系统的性能，大多数高速的设计理论也要最终经过 Layout得以实现并验证，由此可见，布线在高速PCB设计中是至关重要的。下面将针对实际布线中可能遇到的一些情况，分析其合理性，并给出一些比较优化的走线策略。主要从直角走线，差分走线，蛇形线等三个方面来阐述。

　　想要获得更多新鲜PCB设计资料，请关注PCB设计技术专题。

　　1． 直角走线

　　直角走线一般是PCB布线中要求尽量避免的情况，也几乎成为衡量布线好坏的标准之一，那么直角走线究竟会对信号传输产生多大的影响呢？从原理上说，直角走线会使传输线的线宽发生变化，造成阻抗的不连续。其实不光是直角走线，顿角，锐角走线都可能会造成阻抗变化的情况。

　　直角走线的对信号的影响就是主要体现在三个方面：一是拐角可以等效为传输线上的容性负载，减缓上升时间；二是阻抗不连续会造成信号的反射；三是直角尖端产生的EMI。

　　很多人对直角走线都有这样的理解，认为尖端容易发射或接收电磁波，产生EMI，这也成为许多人认为不能直角走线的理由之一。然而很多实际测试的结果 显示，直角走线并不会比直线产生很明显的EMI。也许目前的仪器性能，测试水平制约了测试的精确性，但至少说明了一个问题，直角走线的辐射已经小于仪器本 身的测量误差。

　　总的说来，直角走线并不是想象中的那么可怕。至少在GHz以下的应用中，其产生的任何诸如电容，反射，EMI等效应在TDR测试中几乎体现不出来， 高速PCB设计工程师的重点还是应该放在布局，电源/地设计，走线设计，过孔等其他方面。当然，尽管直角走线带来的影响不是很严重，但并不是说我们以后都 可以走直角线，注意细节是每个优秀工程师必备的基本素质，而且，随着数字电路的飞速发展，PCB工程师处理的信号频率也会不断提高，到10GHz以上的 RF设计领域，这些小小的直角都可能成为高速问题的重点对象。

　　2． 差分走线

　　差分信号（Differential Signal）在高速电路设计中的应用越来越广泛，电路中最关键的信号往往都要采用差分结构设计，什么另它这么倍受青睐呢？在PCB设计中又如何能保证其良好的性能呢？带着这两个问题，我们进行下一部分的讨论。

　　何为差分信号？通俗地说，就是驱动端发送两个等值、反相的信号，接收端通过比较这两个电压的差值来判断逻辑状态"0"还是"1"。而承载差分信号的那一对走线就称为差分走线。

　　差分信号和普通的单端信号走线相比，最明显的优势体现在以下三个方面：

　　a.抗干扰能力强，因为两根差分走线之间的耦合很好，当外界存在噪声干扰时，几乎是同时被耦合到两条线上，而接收端关心的只是两信号的差值，所以外界的共模噪声可以被完全抵消。

　　b.能有效抑制EMI，同样的道理，由于两根信号的极性相反，他们对外辐射的电磁场可以相互抵消，耦合的越紧密，泄放到外界的电磁能量越少。

　　c. 时序定位精确，由于差分信号的开关变化是位于两个信号的交点，而不像普通单端信号依靠高低两个阈值电压判断，因而受工艺，温度的影响小，能降低时序上的误差，同时也更适合于低幅度信号的电路。目前流行的LVDS（low voltage differential signaling）就是指这种小振幅差分信号技术。

　　3． 蛇形线

　　蛇形线是Layout中经常使用的一类走线方式。其主要目的就是为了调节延时，满足系统时序设计要求。设计者首先要有这样的认识：蛇形线会破坏信号质量，改变传输延时，布线时要尽量避免使用。但实际设计中，为了保证信号有足够的保持时间，或者减小同组信号之间的时间偏移，往往不 得不故意进行绕线。

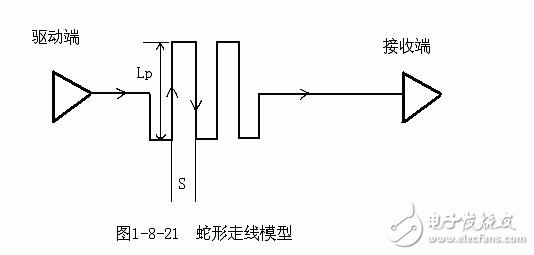
　　那么，蛇形线对信号传输有什么影响呢？走线时要注意些什么呢？其中最关键的两个参数就是平行耦合长度（Lp）和耦合距离（S），如图1-8-21所示。很明显，信号在蛇形走线上传输时，相互平行的线段之间会发生耦合，呈差模形式，S越小，Lp越大，则耦合程度也越大。

　　二、PCB阻抗控制

　　随着 PCB 信号切换速度不断增长，当今的 PCB 设计厂商需要理解和控制 PCB 迹线的阻抗。相应于现代数字电路较短的信号传输时间和较高的时钟速率，PCB 迹线不再是简单的连接，而是传输线。

在实际情况中，需要在数字边际速度高于1ns或模拟频率超过300Mhz时控制迹线阻抗。PCB 迹线的关键参数之一是其特性阻抗（即波沿信号传输线路传送时电压与电流的比值）。印制电路板上导线的特性阻抗是电路板设计的一个重要指标，特别是在高频电路的