电流源设计小Tips（二）：如何解决运放振荡问题

网络，使Rsample上的电压进入Vin-之前由RF、Rm和Cm进行积分滤波，使输出电流中高次谐波成分无法（或大部分无法）进入运放。对于电子负载，积分补偿更为重要。

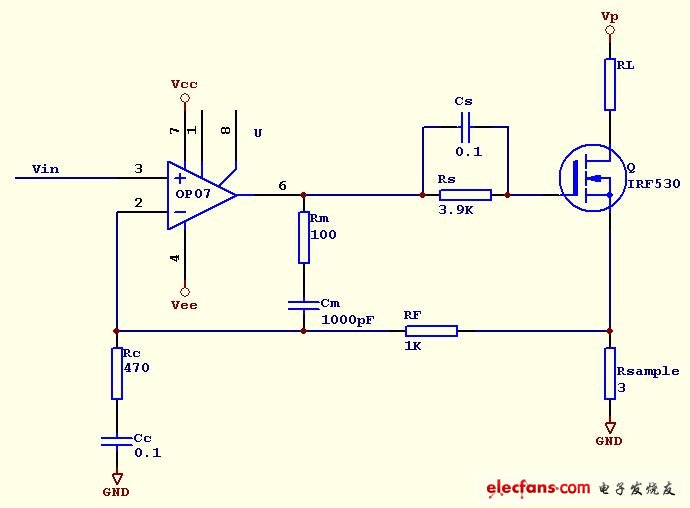
　　由于RF、Rm和Cm构成积分器，因而称为积分补偿。积分补偿的0dB频率fi0dB由RF和Cm决定fi0dB=1/2piRFCm。

　　大于0dB频率的纹波成分受到衰减，直至达到Rm和Cm确定的回转（零点）频率fiz=1/2piRmCm。回转的作用在于不过分降低系统对高频的反应能力。

　　0dB频率至少应低于诱发振荡的纹波频率10倍，已达有效衰减。

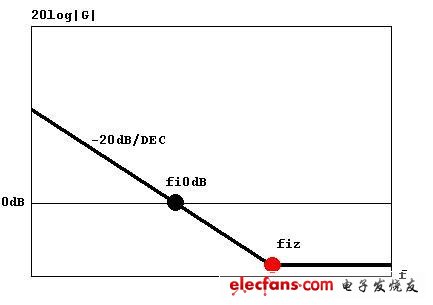
　　很多电路不使用Rm，即没有回转频率。那一定有Cm很小（100pF左右）的前提，否则如果Cm很大，积分频响曲线在高频段衰减过于严重，将造成系统高频控制力下降。对于Vp性能不太好的情况，Cm可能取值很大，因此Rm是必要的。

　　显然，积分器0dB频率越低，系统越稳定，但也会由于Rm、Cm和Rc、Cc构成的局部反馈使系统瞬态性能降低，因此适可而止。

　　积分补偿没有固定的经验值，如果Vp质量较好，Cm甚至可以降至22pF，反之，如果Vp质量很差（例如电子负载通常见到的情况），Cm可增大至1uF。

　　此外Cm的选择还与运放GBW有关，GBW越高（当然要有频率足够高的MOSFET配合），系统对于高频的控制能力越强，Cm可越小。

　　Rm决定回转频率，通常回转频率高于0dB频率10倍以上，因此Rm大致为1/10RF=100 Ohm。

　　因此，如果可能，一定首先改善Vp质量。

　　好在本次只做100mA的电流源，一个7824或LM317就搞定了。在此情况下Cm=1000pF足矣。fi0dB=160kHz，fiz=1.6MHz，160kHz频率以上由Vp造成的电流纹波/噪声可由输出减振器网络消除。

　　本次增加成本：

　　100 Ohm电阻 1只 单价0.01元，合计0.01元

　　1000pF/50V电容 1只 单价0.03元，合计0.03元

　　合计0.04元

　　合计成本：9.55元

　　题外话：
　　Rm、Cm、Rc和Cc构成的局部反馈问题至今悬而未决，用拉普拉斯变换，无论如何计算，运放开环直流增益都会下降至（Cs+Cm）/Cm，但实际上直流时电容是开路，运放开环直流增益不受影响。

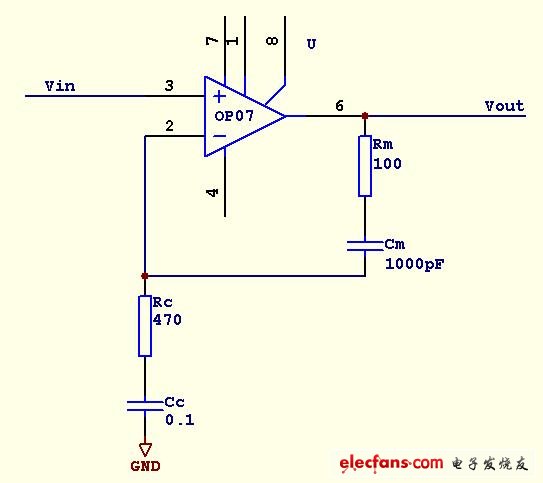
　　也许是拉普拉斯变换对直流力不从心，细细想来，倒是一个简单的问题，1/0不是无穷大，而是没有意义。

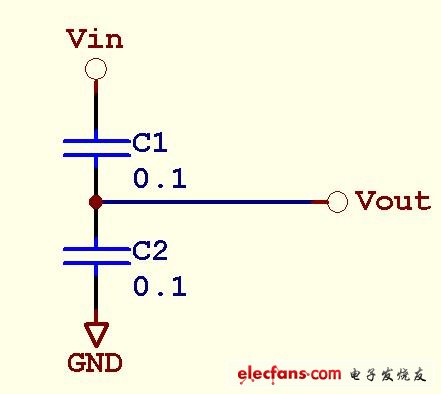
　　考虑以下的电路，Vin为直流电压，Vout是多少呢？如果用容抗计算Vout=1/2Vin，但实际上Vout=任意值。因为直流下电容没有容抗概念。

　　避免轻微的超调过冲和常规电压接口

　　由于噪声增益补偿的问题，电流源在阶跃激励下会有轻微的超调过冲，稍严重一点儿在示波器上能看到逐渐衰减的超调振荡。

　　虽然不严重，但追求完美即完善细节，尽量做得比对手好一点。

　　如果电流源看不到陡峭的上升沿，也就不存在这个问题了。

　　蒙蔽它。只需一个低通滤波器。

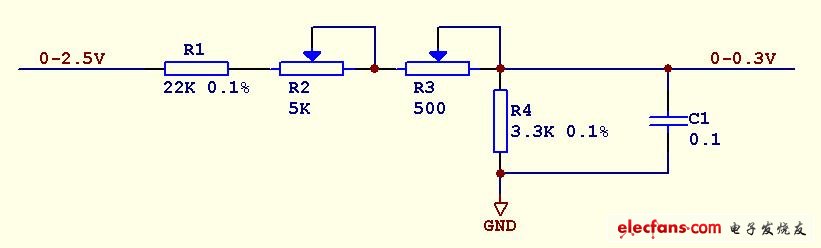
　　恰好正需要一个常规电压接口，0—0.3V估计不是标准的电压，标准电压一般都是2.5V/5V（DAC、基准）或7V（更好的基准）。

　　电阻分压降压即可，以2.5V为例。

　　（2.5/0.3）-1=7.33，如果对地电阻R4为3.3k Ohm，水平电阻为24.2k Ohm，其中设置微调R2=5k Ohm + R3=500 Ohm电位器，固定电阻R1取值22k Ohm。

　　对地电阻并电容C1，获得低通滤波器，转折频率f=1/2piC1（R4//（R1+R2+R3））《zc=1kHz，C1》0.054uF，实际取0.1uF。

　　R1和R4影响电流源的温度性能，因此必须使用低温漂电阻。

　　此时Iin的影响就应降至最低。

　　本次增加成本：

　　22k Ohm 0.1% 1/4W 25ppmmax金属膜电阻 1只 单价0.50元，合计0.50元。

　　3.3k Ohm 0.1% 1/4W 25ppmmax金属膜电阻 1只 单价0.50元，合计0.50元。

　　5k Bouns 10圈精密微调3296电位器 1只 单价2.00元，合计2.00元

　　500 Ohm Bouns 10圈精密微调3296电位器 1只 单价2.00元，合计2.00元

　　0.1uF/50V电容 1只 单价0.03元，合计0.03元

　　合计5.03元

　　合计成本14.58元