如何从代码的角度解读深度学习

　　在本文中会站在代码的角度上为你解读深度学习的前世今生，文章根据六段代码从不同的阶段解说，并将相关的代码示例都上传展示了。如果你是FloydHub新手，在本地计算机上的示例项目文件夹中安装好CLI之后，可以使用以下命令在FloydHub上启动项目：

　　接下来我们一起跟着原作者细读这六段极富历史意义历史的代码，最小二乘法

　　最小二乘法最初是由法国数学家勒让德（Adrien-Marie Legendre）提出的，他曾因参与标准米的制定而闻名。勒让德痴迷于预测彗星的位置，基于彗星曾出现过的几处位置，百折不挠的计算彗星的轨道，在经历无数的测试后，他终于想出了一种方法平衡计算误差，随后在其1805年的著作《计算慧星轨道的新方法》中发表了这一思想，也就是著名的最小二乘法。

　　勒让德将最小二乘法运用于计算彗星轨道，首先是猜测彗星将来出现的位置，然后计算这一猜测值的平方误差，最后通过修正猜测值来减少平方误差的总和，这就是线性回归思想的源头。

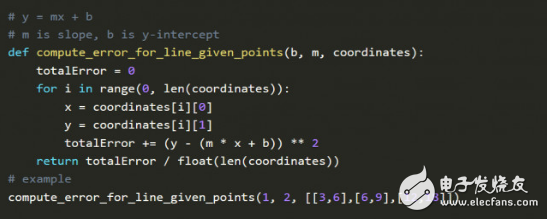
　　在Jupyter notebook上执行上图的代码。 m是系数，b是预测常数，XY坐标表示彗星的位置，因此函数的目标是找到某一特定m和b的组合，使得误差尽可能地小。

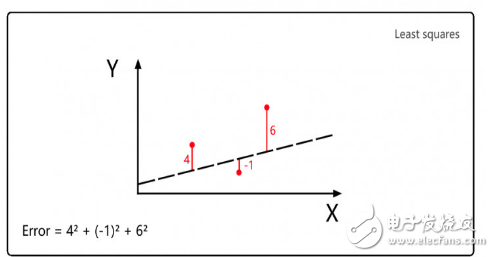
　　这也是深度学习的核心思想：给定输入和期望输出，寻找两者之间的关联性。

　　梯度下降

　　勒让德的方法是在误差函数中寻找特定组合的m和b，确定误差的最小值，但这一方法需要人工调节参数，这种手动调参来降低错误率的方法是非常耗时的。在一个世纪后，荷兰诺贝尔奖得主彼得·德比（Peter Debye）对勒让德的方法进行了改良。

　　假设勒让德需要修正一个参数X，Y轴表示不同X值的误差。勒让德希望找到这样一个X，使得误差Y最小。如下图，我们可以看出，当X=1.1时，误差Y的值最小。

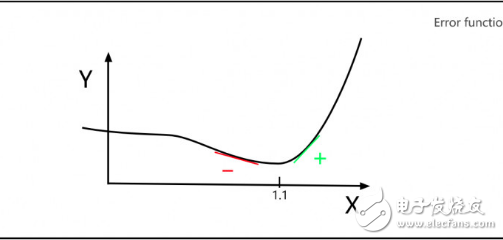
　　如上图，德比注意到，最小值左边的斜率都是负数，最小值右边的斜率都是正数。因此，如果你知道任意点X值所处的斜率，就能判断最小的Y值在这一点的左边还是右边，所以接下来你会尽可能往接近最小值的方向去选择X值。

　　这就引入了梯度下降的概念，几乎所有深度学习的模型都会运用到梯度下降。

　　假设误差函数 Error = X5 - 2X3 - 2

　　求导来计算斜率：

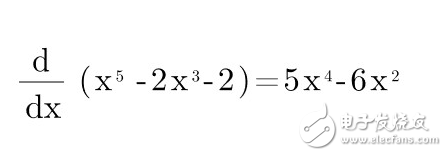
　　如果读者需要补充导数的知识，可以学习Khan Academy的视频。

　　下图的python代码解释了德比的数学方法：

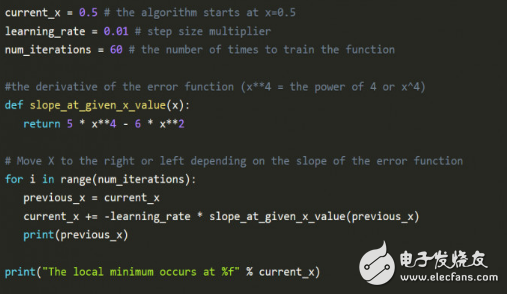
　　上图代码最值得注意的是学习率 learning_rate，通过向斜率的反方向前进，慢慢接近最小值。当越接近最小值时，斜率会变得越来越小，慢慢逼近于0，这就是最小值处。

　　Num_iteraTIons 表示在找到最小值前估算的迭代次数。

　　运行上述代码，读者可以自行调参来熟悉梯度下降。

　　线性回归

　　线性回归算法结合了最小二乘法和梯度下降。在二十世纪五六十年代，一组经济学家在早期计算机上实现了线性回归的早期思想。他们使用穿孔纸带来编程，这是非常早期的计算机编程方法，通过在纸带上打上一系列有规律的孔点，光电扫描输入电脑。经济学家们花了好几天来打孔，在早期计算机上运行一次线性回归需要24小时以上。

　　下图是Python实现的线性回归。

　　梯度下降和线性回归都不是什么新算法，但是两者的结合效果还是令人惊叹，可以试试这个线性回归模拟器来熟悉下线性回归。

　　感知机

　　感知机最早由康奈尔航空实验室的心理学家弗兰克·罗森布拉特（Frank Rosenblatt）提出，罗森布拉特除了研究大脑学习能力，还爱好天文学，他能白天解剖蝙蝠研究学习迁移能力，夜晚还跑到自家屋后山顶建起天文台研究外太空生命。1958年，罗森布拉特模拟神经元发明感知机，以一篇《New Navy Device Learns By Doing》登上纽约时报头条。

　　罗森布拉特这台机器很快吸引了大众视线，给这台机器看50组图片（每组由一张标识向左和一张标识向右的图片组成），在没有预先设定编程命令的情况下，机器可以识别出图片的标识方向。

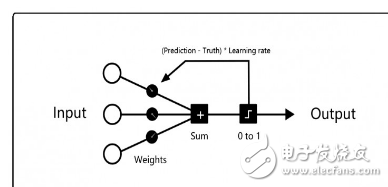
　　每一次的训练过程都是以左边的输入神经元开始，给每个输入神经元都赋上随机权重，然后计算所有加权输入的总和，如果总和是负数，则标记预测结果为0，否则标记预测结果为1。

　　如果预测是正确的，不需要修改权重；如果预测是错误的，用学习率（learning_rate）乘以误差来对应地调整权重。

　　下面我们来看看感知机如何解决传统的或逻辑（OR）。

　　Python实现感知机：

等人们对感知机的兴奋劲头过后，马文·明斯基（Marvin Minsky）和西摩·帕普特（Seymour Papert） 打破了人们对这一思想的崇拜。当时明斯基和帕普特都在MIT的AI实验室工作，他们写了一本书证明感知机只能解决线性问