如何从代码的角度解读深度学习
题,指出了感知机无法解决异或问题(XOR)的缺陷。很遗憾,罗森布拉特在两年后的一场船难中遇难离世。
在明斯基和帕普特提出这一点的一年后,一位芬兰的硕士学生找到了解决非线性问题的多层感知机算法。当时因为对感知机的批判思想占主流,AI领域的投资已经干枯几十年了,这就是著名的第一次AI寒冬。
明斯基和帕普特批判感知机无法解决异或问题(XOR,要求1&1返回0):
对于左图的OR逻辑,我们可以通过一条线分开0和1的情形,但是对于右边的XOR逻辑,无法用一条线来划分。
人工神经网络
到了1986年,鲁梅尔哈特(David Everett Rumelhart)、杰弗里·辛顿(Geoffrey Hinton)等人提出反向传播算法,证明了神经网络是可以解决复杂的非线性问题的。当这种理论提出来时,计算机相比之前已经快了1000倍。让我们看看鲁梅尔哈特等人如何介绍这篇具有重大里程碑意义的论文:
我们为神经元网络提出了一种新的学习过程——反向传播。 反向传播不断地调整网络中的连接权重,最小化实际输出与期望输出之间的误差。 由于权重调整,我们加入了隐藏神经元,这些神经元既不属于输入层,也不属于输出层,他们提取了任务的重要特征,并对输出进行了正则化。反向传播这种创造有效特征的能力,将其与之前的算法(如感知器收敛过程)区别开来。
Nature 323,533-536(1986年10月9日)
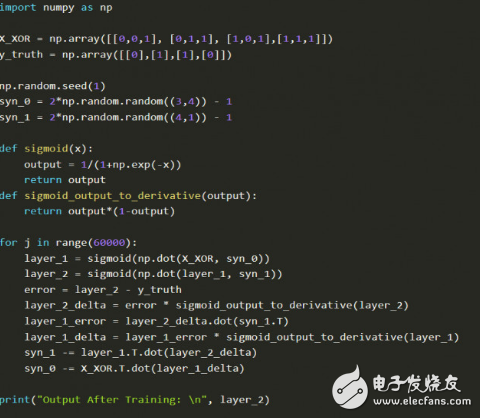
为了理解这篇论文的核心,我们实现了DeepMind大神Andrew Trask的代码,这并不是随机选择的代码,这段代码被Andrew Karpathy斯坦福的深度学习课程、Siraj Raval在Udacity的课程中采用。更为重要的是,这段代码体现的思想解决了XOR问题,融化了AI的第一个冬季。
在我们继续深入之前,读者可以试试这个模拟器,花上一两个小时来熟悉核心概念,然后再读Trask的博客,接下来多熟悉代码。注意在X_XOR数据中增加的参数是偏置神经元(bias neurons),类似于线性函数中的常量。
这里结合的反向传播,矩阵乘法和梯度下降可能会绕晕你,读者可以通过可视化过程来理解。先注重去看背后的逻辑,不要想着一下子就能完全参透全部。
另外,读者可以看看Andrew Karpathy的反向传播那一课,玩转一下可视化过程,读读迈克尔·尼尔森(Michael Nielsen)的《神经网络与深度学习》书上这一章。
深度神经网络
深度神经网络指的是除了输入层和输出层,中间还存在多层网络的神经网络模型,这一概念首先由加利福尼亚大学计算机系认知系统实验室的Rina Dechter提出,可参考其论文《Learning While Searching in Constraint-SaTIsfacTIon-Problems》,但深度神经网络的概念在2012年才得到主流的关注,不久后IBM IBM Watson在美国智力游戏危险边缘(eopardy)取得胜利,谷歌推出了猫脸识别。
深层神经网络的核心结构仍保持不变,但现在开始被应用在不同的问题上, 正规化也有很大的提升。一组最初应用于简化噪音数据的数学函数,现在被用于神经网络,提高神经网络的泛化能力。
深度学习的创新很大一部分要归功于计算能力的飞速提升,这一点改进了研究者的创新周期,那些原本需要一个八十年代中期的超级计算机计算一年的任务,今天用GPU只需要半秒钟就可以完成。
计算方面的成本降低以及深度学习越来越丰富的库资源,使得大众也可以走进这一行。我们来看一个普通的深层学习堆栈的例子,从底层开始:
GPU 》 Nvidia Tesla K80。通常用于图像处理,对比CPU,他们在深度学习任务的速度快了50-200倍。
CUDA 》 GPU的底层编程语言。
CuDNN 》 Nvidia优化CUDA的库
Tensorflow 》 Google的深度学习框架
TFlearn 》 Tensorflow的前端框架
我们来看一个数字分类的例子(MNIST数据集),这是一个入门级的例子,深度学习界的"hello world"。
在TFlearn中实现:
有很多经典的文章解释了MNIST问题,参考Tensorflow文档、JusTIn Francis的文章以及Sentdex发布的视频。
如果读者还想对TFlearn有进一步了解,可参考作者Emil Wallner之前的博客文章。
总结
如同上图的TFlearn示例,深度学习的主要思想仍然很像多年前罗森布拉特提出的感知机,但已经不再使用二进制赫维赛德阶跃函数(Heaviside step function),今天的神经网络大多使用Relu激活函数。在卷积神经网络的最后一层,损失设置为多分类的对数损失函数categorical_crossentropy,这是对勒让德最小二乘法的一大改良,使用逻辑回归来解决多类别问题。另外优化算法Adam则起源于德比的梯度下降思想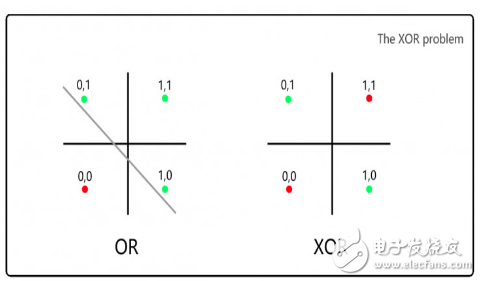



- 机器学习算法盘点:人工神经网络、深度学习(07-02)
- 2016年人工智能与深度学习领域的十大收购(07-26)
- AI/机器学习/深度学习三者的区别是什么?(09-10)
- 深度学习的硬件架构解析(10-18)
- 麻省理工科技评论评选的14大医疗领域突破科技(上)(10-14)
- 探秘机器人是如何进行深度学习的(09-18)
