传输线设计是高频有线网络、射频微波工程、雷射光纤通信等光电工程的基础,为了能让能量可以在通信网路中无损耗地传输,良好的传输线设计是重要关键。
无线通信加上视频技术将成为未来的明星产业,要达到这个目标,负责传送射频微波信号的介质除空气之外,就是高频的传输线。人类目前无法控制大气层,但是可以控制射频微波传输线,只要设法使通信网路的阻抗能相互匹配,发射能量就不会损耗。本文将从阻抗匹配的角度来解析射频微波传输线的设计技术。
驻波比(SWR)
两频率相同、振幅相近的电磁波能量流(energy flows)面对面地相撞(impinge)在一起,会产生驻波(standing wave),这种电磁波的能量粒子在空间中是处于静止(stand)状态(motionless)的,此暂停运动的时间长度比两电磁波能量流动的时间要长。因为驻波的能量粒子是静止不动的,所以,没有能量流进驻波或从驻波流出来。上述叙述较抽象,但是这里举个类似的例子,就可说明什么是驻波:做个物理实验,将两个口径、流速都相同的水管,面对面相喷,在两水管之间将会激起一个上下飞奔的水柱,这个水柱就是驻波。如果是在无地心引力的空间中,这个水柱将静止在那里不会坠地。
电磁波在传输在线流动,入射波和反射波相遇时就会产生驻波。驻波比(standing wave rate;SWR)是驻波发生时最大电压和最小电压的比值(VSWR),或最大电流和最小电流的比值(公式一):
SWR = (VO + VR)/ (VO - VR) = (IO + IR)/ (IO - IR) = 1+|Γ|/ 1-|Γ|
WR可以被用来判定传输线阻抗匹配的情况:当SWR=1时,表示没有反射波存在,电磁波能量能完全传递到负载上,也就是传输线阻抗完全匹配;当SWR=∞时,表示VO = VR或IO = IR,电磁波能量完全无法传递到负载上,传输线阻抗完全不匹配。SWR测量仪是高频传输线、发射机(transmitter)、天线工程师常使用的参数,与它类似的是应用在有线电视缆线(Cable TV cable)的「返回耗损(Return Loss)」或称作dBRL。两者的差别有二:(1)dBRL=0表示阻抗完全不匹配,dBRL=∞表示阻抗完全匹配。(2)SWR测量仪是以发射机为信号来源,自己并没有发射源,但dBRL测量仪是用自己的发射源来测量缆线的阻抗匹配情况。
'史密斯图(Smith Chart)介绍:
为了达到阻抗匹配的目的,必须使用史密斯图。此图为P. Smith于1939年在贝尔实验室发明的,直到现在,它的图形仍然被广泛地应用在分析、设计和解决传输线的所有问题上。它能将复数的负载阻抗(complex load impedance)映射(map)到复数反射系数(complex reflection coefficients)的Γ平面上,这种映射过程称作「正常化(normalization)」。如(图一)所示,大小不同的圆弧代表实数(rL)与虚数(xL)的大小,越往右边阻抗越大,越往左边阻抗越小。乍看之下,史密斯图很类似极坐标(polar coordinate),不过,它的X-Y轴坐标分别是Γr和Γi,而且Γ= |Γ|ejθr =Γr + jΓi ,r代表实数(real number),i代表虚数(image number)。在图一中,中心线为电阻值,中心线上方区域为感抗值,中心线下方区域为容抗值,直径和中心线重迭的圆代表不同的实数(rL),中心线两旁的圆弧代表不同的虚数(rL)。正常化负载阻抗(normalized load impedance)zL = ZL/Z0= 1+Γ/1-Γ,zL= rL+jxL,其实zL就是史密斯图上的复数,它没有计量单位(dimensionless),是由实数rL和虚数xL构成的。负载阻抗ZL就是由小写的zL映射到复数反射系数Γ平面上的。史密斯图的圆心代表Γ=0,zL=1,ZL= Z0,负载阻抗匹配,如(图三)所示。
将阻抗转换到Γ平面后,就能得出代表传输线匹配或不匹配的反射系数(公式二):
Γ=
ZL-Z0
ZL+Z0
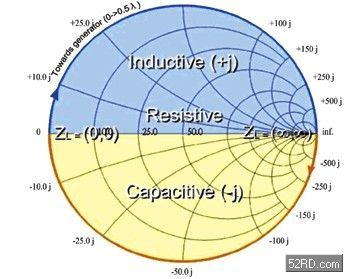
图一 史密斯Z坐标图
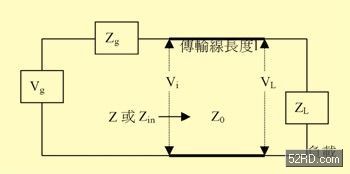
图二 无耗损传输线电路
在上式中,Γ就是(电压)反射系数,它的定义是:反射波(reflected voltage wave)的电压振幅与入射波(incident voltage wave)的电压振幅之比值;ZL是负载阻抗(load impedance),Z0是特性阻抗(characteristic impedance)。当ZL = Z0时,达到阻抗匹配,Γ为零。如(图二)所示,假设ZL = Z0,电压源(Vg)产生的功率几乎可以完全供给负载使用,而从负载反射回电压源的功率非常小。对负载应用而言,必须设法求得特性阻抗,并使负载阻抗等于它。亦即,在图三中的Γ必须尽量在绿色区域之中。图三也称为珈玛坐标图(Gamma-centric chart),有别于图一的Z坐标图(Z- centric chart)。



