从阻抗匹配解析射频传输线技术

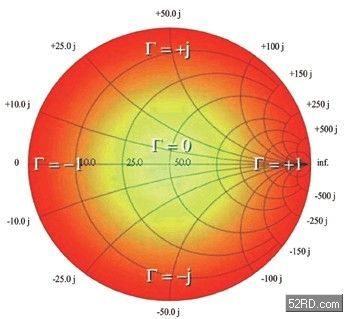
    图三　史密斯Γ坐标图
　

    理想的无耗损（lossless）传输线是依据下列公式来转换负载阻抗ZL（公式三）：
    Z = Z0
    ZL cos(l 2/) + j Z0 sin(l 2/)
    Z0 cos(l 2/) + j ZL sin(l 2/)

    在上式中，l是无耗损传输线的长度，l 2/是此传输线长度与波长相比的角度值（radian）。从上式和图二中，可以得出下列重要的结论：

    (1)如果ZL = Z0，则无论传输线的长度大小为何，输入端阻抗Z或Zin永远等于特性阻抗Z0。

    (2)Z是以/2为单位做周期变化。

    (3)正常化输入阻抗（normalized input impedance）zin=Zin/Z0= 1+Γl/1-Γl，其中，Γl 的振幅与电压反射系数Γ的振幅一样，但是相角差2βl（β=2π/λ），l是传输线长度。所以，Γl被称为「相移电压反射系数（phase-shifted voltage reflection coefficient）」，而且Γl =Γe-j2βl。因此，如果Γ转换成（transform）Γl，zL就被转换为zin了，在史密斯图上的反射系数角位（angle of reflection coefficient in degrees）是以顺时钟方向，随传输线长度l由0最大增加到0.5λ，这个方向上的刻度称为「波长朝产生器（wavelengths toward generator；WTG）」方向的刻度，有别于逆时钟方向的「波长朝负载（wavelengths toward load；WTL）」方向的刻度。

    (4)在史密斯图的圆心处划一个圆，它将和实数轴与虚数轴相交于数个点，每个点与圆心的距离相等，这个圆称作「常数｜Γ｜圆」；也叫作「驻波率（standing-wave ratio；SWR）圆」，这是因为驻波率S=1＋｜Γ｜/ 1－｜Γ｜。
如果今天已知传输线长度l和zL，利用史密斯图，就可以很快地求出zin。

    (5)纯电阻窄频匹配（resistive narrowband match）时，驻波率刚好等于rL和驻波率圆相交的右边接点Pmax。虽然rL和驻波率圆相交的接点有两个Pmax和Pmin，但是左边接点Pmin的rL值小于1，而且驻波率必须大于或等于1，所以Pmin不予考虑。藉由史密斯图和已知的负载阻抗，就可以很快地求得在传输在线最大电压或最小电流、最小电压或最大电流的位置。

    上述功能，说明了利用史密斯图就能得到负载的复数阻抗之匹配值。 

    阻抗（impedance）和导纳（admittance）的转换

    在解决某些类型的传输线问题时，为求方便起见都使用导纳来表示。导纳是阻抗的倒数，其数学定义是：Y=1/Z=G+jB，G称作电导（conductance），B称作电纳。正常化导纳y是正常化阻抗z的倒数，所以y=1-Γ/1+Γ。如果在史密斯图上顺时钟移转λ /4（互成反方向），zL将转换成zL。虽然，Y参数（=[Y][V]）的导纳和Z参数（[V]=[Z]）的阻抗，都只能代表低频电路的特性，但是与代表高频电路特性的S参数（[V-]=[S][V+]）类似的Y参数是由四种导纳变数构成的，藉由Y参数（一般是从所测量的S参数转换而来）可以得到晶体管闸阻抗之值，这在深次微米设计中是非常重要的。S参数是被用来表示射频微波多端口网络（multiple network）中多电波的电路特性。 

    ■史密斯图应用范例

    应用上述原理和方法，将一般的50-Ω无耗损传输线之一端接有负载阻抗ZL =（25+j50）Ω，使用史密斯图可以得到：

    (1)电压反射系数：zL= ZL/Z0=（25+j50）/50=0.5+j1，从史密斯图中可以查出反射系数的相角为83°，用尺可以量得反射系数的振幅为0.62；所以，电压反射系数Γ= 0.62ej83°。

    (2)电压驻波比（SWR）：使用圆规在史密斯图上，以Γ=0为圆心，划一个圆（驻波率圆）通过0.62ej83°，这个圆和Γr相交在两点，其中一点的rL值大于1，为4.26，亦即电压驻波比S=4.26。

    (3)距负载最近的最大电压与最小电压的位置：最大电压在驻波率圆和Γr相交的点上，查史密斯图，此点的位置是0.25λ，负载的位置是0.135λ，所以它和负载的距离是lmax=0.25λ-0.135λ=0.115λ；最小电压和最大电压的距离差0.25λ，所以它和负载的距离是lmin=0.115λ+0.25λ=0.365λ。

    (4)若此传输线长度为3.3λ，可求出其输入阻抗和输入导纳：3.3λ除以0.5λ后剩余0.3λ，从负载阻抗在史密斯图上的位置顺时钟移动（WTG）0.3λ，就是输入阻抗的位置。因此，输入阻抗的位置是在0.135λ+0.3λ=0.435λ直线上，它与驻波率圆相交于一点，查史密斯图，此点即是正常化输入阻抗zin=0.28-j0.4，经转换可求得输入阻抗Z in=zinZ0=(0.28-j0.4)*50=(14-j20)Ω；从zin顺时钟移动0.25λ并与驻波率圆相交于一点，可以得到正常化输入导纳yin=1.15+j1.7，经转换可求得输入导纳Yin=yinY0=yin/ Z0=(1.15+j1.7)/50=（0.023+j0.034）S（全名为Siemens，是导纳的基本计量单位）。

    '使用史密斯图反求负载阻抗

    假设：只知道一条50Ω无耗损传输线的驻波比S=3，距负载最近的最小电压位置是5cm，其次是20cm，试求负载阻抗。

    解决方法：因为最小电压的间距为λ / 2，所以，λ = 40cm。距负载最近的最小电压在史密斯图上的位置就是5/40=0.125λ。在史密斯图上划驻波率圆，半径为3，此圆与Γr相交于两点，rL值小于1的点就是距负载最近的最小电压，在驻波率圆上，从此点逆时钟移动0.125λ，可以得到负载的正常化阻抗zL=0.6 - j0.8。经转换后，就可得出负载阻抗ZL=Z0*zL=(30 - j40)Ω。

    阻抗匹配

    阻抗匹配是电路学里的重要议题，也是射频微波电路的重点。一般的传输线都是一端接电源，另一端接负载，此负载可能是天线或任何具有等效阻抗ZL的电路。传输线阻抗和负载阻抗达到匹配的定义，简单说就是：Z0=ZL。在阻抗匹配的环境中，负载端是不会反射电波的，换句话说，电磁能量完全被负载吸收。因为传输线的主要功能就是传输能量和传送电子讯号或数字数据，一个阻抗匹配的负载和电路网络，将可确保传输到最终负载的电磁能量值能达到最大量。 

    最简单的阻抗匹配方法是设计负载电路使其满足ZL= Z0的条件。可惜这是理想的情况，在设计实务上，因为负载电路必须先满足其它必需的条件，否则负载电路就无法提供应用所需的性能，这通常都会影响它和传输线的阻抗匹配。解决方案是在传输线与最终负载之间加入阻抗匹配网络（impedance-matching network），加入此网络的目的就是为了减少传输线和此网络之间的电波反射作用。如果阻抗匹配网络是无耗损的，而且其输入阻抗ZL等于传输线的特性阻抗Z0，则能量将可以透过它全部到达负载端。

    阻抗匹配网络可以由数个集成组件（lumped elements）或具有特定长度和终端方式（短路或开路）的数节（sections）传输线构成。若是使用集成组件，通常是选用电容和电感，而不用电阻，这是为了避免奥姆耗损（ohmic losses）。因为阻抗匹配网络必须将负载阻抗ZL= RL +jXL的RL、XL分别与传输线特性阻抗Z0相对应的电阻与电抗值匹配，为了达到这两种转换，它至少需要「两个调整参数」或「两个自由度（two degrees of freedom）」。(图四)是单株短路线（shorted single-stub）阻抗匹配网络，其等效电路如(图五)所示。两个自由度是由图四中，长度各为d和l的两节传输线提供的。