基于Android的车载导航系统的研究与设计

　　接着将Criteria的参数传递给LocationManager对象。然后启动GPS定位功能，LocationManager对象就开始通过自身的函数来获取经纬度和其他一些数据。其获取数据的方法如下所示：

① 对于经纬度，getLatitude()返回维度数据，getLongitude()返回经度数据；
② 对于方向，hasBearing()判断是否有方向数据，而getBearing()则以度为单位返回其值；
③ 对于海拔高度，hasAltitude()判断是否有海拔数据，而getAltitude下则以m为单位返回海拔数据；
④ 对于速度，hasSpeed()判断是否有速度值，而getSpeed()则以m/s为单位返回速度值。
⑤ 最后，LocationManager对象返回的数据及时地更新在电子地图上，并且随着物体和时间位置的变化，开发者可以利用LocationManager，使用定位监听器LocationListener根据时间和物体移动距离进行数据更新。

3.2　地图匹配算法设计

　　地图匹配以某个车辆位置点或某段车行轨迹曲线作为待匹配样本，以该点或该轨迹曲线附近的所有道路上的位置点或道路曲线作为模板，通过待匹配样本或模板间的匹配，选择相似度最高的匹配样本或模板作为匹配结果。最后根据匹配结果校正定位模块的定位误差。车载导航系统中将车辆定位显示在电子地图上时，应该根据车辆的行驶方向，将车辆定位显示于某一道路上。但是，由于各种误差(主要是定位技术的误差)，电子地图上显示的车辆会偏离实际的道路，失去其导航的功能；而地图匹配这一软件技术能校正定位技术的误差，使车辆位置准确地显示在电子地图上。

　　可用来判断车辆当前可能在哪条路段上行驶的信息主要有3个：当前车辆定位点距候选路段的投影距离、车辆当前行驶方向与候选路段方向的夹角以及候选路段与前一匹配路段的几何拓扑关系。一般来讲，投影距离和方向夹角越小的候选路段成为匹配路段的可能性越大，反之亦然。此外，与前一匹配路段相同或拓扑相连的候选路段成为匹配路段的可能性大，其余的可能性小。车辆在行驶的过程中，把GPS原始定位点向各待匹配路段作投影，可计算GPS原始定位点与待匹配路段之间的最短距离ri(i=1,…,n)；另外车辆行驶方向与各待匹配路段之间的夹角θi(i=1,…,n)也可以得到，进而计算各待匹配路段的匹配值λi(i=1,…,n)。

　　地图匹配算法在进行匹配时的步骤如下：
① 通过特征提取把所有的待匹配路段分析、描述，提取出相应的匹配因子。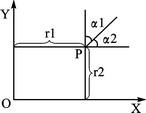

图2　距离与夹角示意图

② 计算定位点P到各个待匹配路段的最短距离。距离与夹角示意图如图2所示。其中r1、r2为要求的最短距离；α1、α2为所求夹角。根据匹配规则，依次计算定点P到各个待匹配路段的匹配值。
③ 把匹配值中最小的路段作为最终匹配路段，并把在此路段上距离原始定位点最近的点作为最终匹配点。

3.3　电子地图显示模块设计

　　利用Android平台开发导航地图过程中，主要采用Android提供的MapView和MapActivity两个类实现。其中MapView是一个展示地图的视图，它可以获取键盘事件来支持地图的移动和缩放功能，地图可以以不同的形式来显示，如街景模式、卫星模式等，通过setSatellite(boolean) 、setTraffic(boolean)和setStreetView(boolean) 方法，同时也支持多层Overlay的使用。可以在地图上画坐标、写地名、画图片等。

　　MapView只能通过MapActivity来建立，因为MapView需要在后台使用文件系统和网络。所有这些线程需要在Activity的生命周期中被控制。

　　如何利用电子地图功能将GPS模块定位得到的经纬度信息在地图上显示出来呢？地球上的任何一个地点都可以利用经纬度来表示。在Android的类库中，Point类代表了一个地点的经纬度，函数格式为：Pointment(int latitudeE6，int longitudeE6)。E6是微度，即度数乘以1000 000。如果要指定地图地点，须传递一个Point类到地图中。然后调用setMapLocationCenter方法将地图移动到合适的位置，最后调用MapController对象的animateTo方法将该坐标位置设置为地图的中心点。在实际应用中，可以使用zoomTo(int)缩放到需要的级别，同时利用mapView.toggleSatellite()和mapView.toggleTraffic()来获得卫星图和路况图。

3.4　最短导航路径规划算法设计

　　求解最短路径问题的算法中，Dijkstra算法是国内外公认的比较成功的算法，该算法通用性强，而且编程实现简单，是目前理论上比较完善、应用最广泛的最短路径分析算法。Dijkstra算法按路径长度的递增次序，逐条产生最短路径。

　　Dijkstra算法的基本思想是：设从顶点V0出发，搜索从它到其他顶点的最短路径。把有向图中的顶点集V分为两个集合，已求出最短路径的顶点集合S，尚未确定最短路径的顶点集合V-S(定义为T)；按最短路径长度递增的顺序逐个把集合T中的顶点加到集合S中，直到和出发点V0有路径相通的所有顶点都包含在集合S中。在整个过程中，V0到集合S中各顶点的最短路径长度都不大于V0到集合T中的任意顶点的最短路径长度。

　　设带权有向图G={V，E}，V={V0，V1，…，Vn-1},用带权的邻接矩阵Arcs表示图G；Arcs[i][j]表示弧<Vi，Vj>上的权值，S表示已求得的从V0出发的最短路径终点的集合；向量D的每个分量D[i]表示当前求得的从始点V0到每个终点Vi的最短路径的长度，算法描述如下：