交互多模型机动目标跟踪算法在车载毫米波雷达防追尾预警系统中的应用
)以得到状态估计。一个模型有效的概率在状态估值和协方差的加权综合计算中有重要作用。IMM的设计参数为:不同匹配和结构的设置模型;不同模型的处理噪声密度(一般来讲,非机动模型具有低水平测量噪声,机动模型具有较高水平的噪声);模型之间的切换结构和转移概率。与其他的机动目标的跟踪算法相比,比如辛格(Singer)算法、输入估计(IE)算法、变维滤波(VD)算法等,交互多模(IMM)算法的优点是它不需要机动检测器监视机动[10],从而不会产生因模型在机动与非机动之间切换而带来的误差。其算法原理如下:
假定有r 个模型:
其中X(k)为目标状态向量,Aj为状态转移矩阵,Gj为系统噪声作用矩阵,Wj(k)是均值为零,协方差矩阵为Qj的白噪声序列。
可用一个马尔可夫链来控制这些模型之间的转换,马尔可夫链的转移概率矩阵为: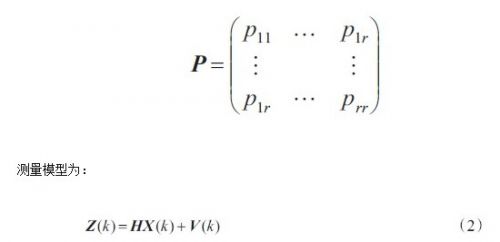
其中Z(k)为量测向量,H为观测矩阵,V(k)为量测噪声,已知其方差为R(k)。W(k)和V(k)是零均值且相互独立。
IMM算法可归纳如下4 个步骤。
步骤1 输入交互:
根据两模型(k-l)时刻的滤波值和模型概率,计算交互混合后的滤波初始值,包括模型1 的滤波初始值:滤波估计值X 01
(k - 1)和估计协方差μ1(k - 1);模型2 的滤波初始值:滤波估计值X 02
(k - 1)和估计误差协方差P02
(k - 1)。设系统在(k-1)时刻模型1 概率为μ1(k - 1),滤波值X1
(k - 1),估计误差协方差为P2(k - 1)。模型2 的概率为μ2(k - 1),滤波值为X 2
(k - 1),系统估计误差协方差为P2(k - 1)。则进一步推广到r 个模型,交互后r模型的滤波初始值为:
步骤2 模型条件滤波:
对应于模型Mj(k),以X 0j
(k - 1|k - 1),P0j(k - 1|k - 1)及Z(k)作为输入进行卡尔曼滤波。
卡尔曼预测方程:
i = 1rΛj(k)cj_,而Λj(k)为观测Z(k)的似然函数: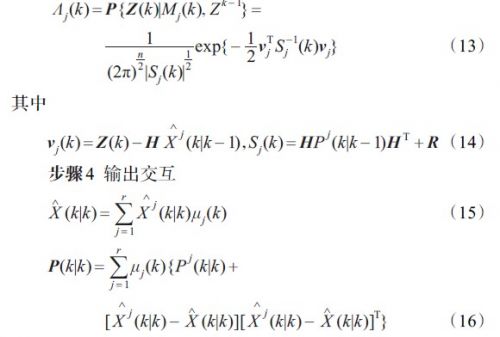
图2 为IMM算法结构原理图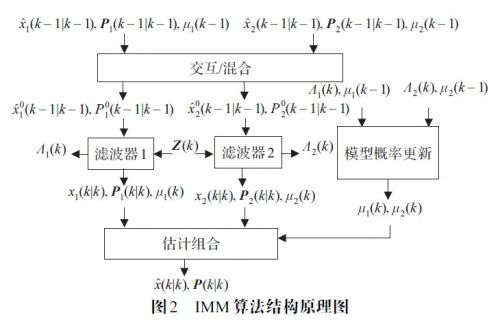
4 车辆运动模型分析与IMM算法跟踪仿真
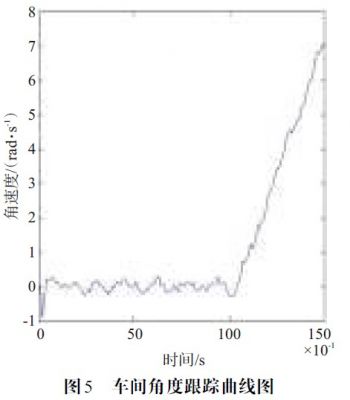
试验设计:考虑两辆车在道路上同向行驶,在0~10 s 时,两车均保持匀速直线运动,由安装在后车上的车载毫米波雷达检测出与前车的距离为100 m,相对速度为-3 m/s,方位角2°。
在10~15 s 时,前车向右偏转,与后车的相对角加速度为1° s2。
后车加速,与前车的纵向相对加速度为a = -1.8 m/s2。雷达的扫描周期为T=0.1 s,系统噪声为σα = 0.3 m/s,σβ = 0.3°/s。量测误差为σ1 = 1 mσ2 = 0.5 m/sσ3 = 0.2°/s。
车辆匀速直线运动模型:

采用蒙特卡洛方法对跟踪滤波器进行仿真分析,仿真次数为400 次。以下运用Matlab7.0 仿真的结果。
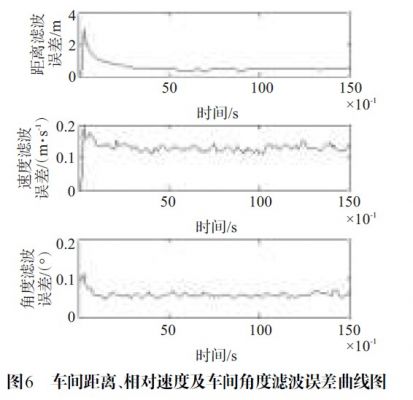
由图3~图6 仿真结果表明,该算法能够有效地跟踪前方车辆的运动信息,并且误差较小,精度较高。
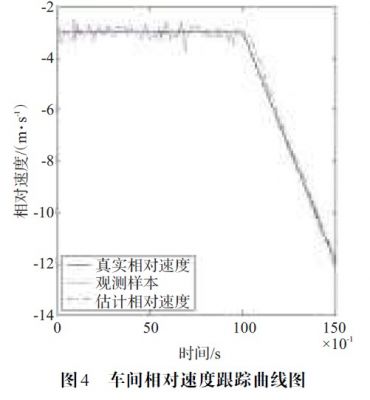
5 总结
重点研究了交互多模型机动目标跟踪算法在车载毫米波雷达防追尾预警系统中的应用,介绍机动目标跟踪算法原理和步骤,并以高速公路上行驶的汽车为对象进行防真,结果表明算法具有结构简单、运算量小、精度较高的优点,能够提高车载雷达防追尾预警系统的使用效率,从而提高车辆驾驶的安全性,具有一定的应用价值。
