基于视觉的智能车转向控制策略

利用上面的关系，可以间接测量出小车与目标引导线之间的偏角,如图4所示。若设AB为基准线，即车的中线；AK为引导线；过F点向y轴做垂线，与基准线AB的交点为C，定义C点为基准位置。在三角形AFC中，角β为基准线与引导线之间的夹角：

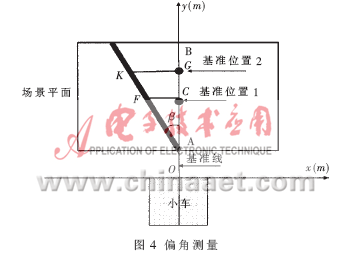
在理想情况下，控制舵机向左偏转β角度即可让小车追随到引导线。但这样计算角度的计算负担很重，简化参考文献[2]中横向偏差的测量方法，在基准位置固定的情况下，可用CF的长度近似表示角度β的大小:

|CF|=K×β (3)

式中，K为一个比例系数。结合图像平面与场景平面之间的关系，定义CF的长度即为偏差，转化到图像平面为:

err=line1-linem (4)

式中, linem为基准位置对应的列值，line1为同行引导线的列值，err为位置偏差。因此，在实际的软件设计中，不必得到真实场景坐标，可以直接对引导线实际位置与基准位置间图像坐标的差(line1-linem)设计控制算法。如增量PID控制器可设计为:

Δu(k)=u(k)-u(k-1)=KP[err(k)-err(k-1)]+KIerr(k)+KD[err(k)-2err(k-1)+err(k-2)]

式中,KP为比例系数，KI为积分系数，KD为微分系数。Δu为舵机给定的增量[7-11]。

2 转向模型

获得道路的位置信息，即获得了此刻小车的转向角。参考文献[11]中的舵机转向模型，在理想状态下，此刻控制舵机使前轮偏转相应角度即可实现小车对道路的跟随。舵机的转向相当于给车一个向心力，在转角不变时，小车做圆周运动；如果控制驱动电机的PWM脉宽不变，则小车做匀速圆周运动，驱动电机的 PWM脉宽对应的小车速度相当于匀速圆周运动的线速度。如图5所示，设车的侧轮距为b，舵机转角为θ，O为车做圆周运动的圆心，R为外轮所对应半径,则每一个转角对应圆周运动的半径[2]如下：

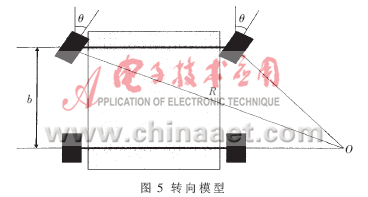
设控制周期为T,小车当前速度为V，α为一个控制周期T内小车沿圆周行驶的弧度数，则有：

由以上模型可以看出，不同的速度和转角会在一个控制周期T内得到不同的弧度，对上述公式离散化后可以得到: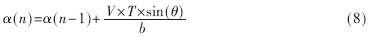

小车在转弯的过程中，舵机转角受多种因素限制(如：小车转向机构造成的转向的延滞、舵机的时间常数等），是一个渐变的过程，而利用公式(8)进行计算的前提是舵机的方向能随控制量的改变而立即改变。为了简化分析，将舵机模型视为仅具有延滞时间TD的延滞环节而忽略其时间常数。如图6所示，由于TD的存在，速度越大，在滞后时间TD内，小车行走的距离越远。

3 转向策略设计

如图7所示，设小车前方距离D处为弯道，小车此刻速度为V，结合图6小车舵机转向理想模型响应曲线，如果让小车在A点入弯，速度必须满足:

D=V×TD (9)

在图4中，对于基准位置1和基准位置2，由道路信息提取的结果，为了保证A点入弯，基准位置2比基准位置1更早地发出转向命令，需要更大的速度才可以在A点入弯，在保证两位置的速度可以安全过弯的前提下，基准位置2得到了更高的入弯速度，所以更早地得到弯道的信息可以提高入弯速度。同时小车要想快速地入弯，必须将基准位置提到一个与此刻速度匹配的位置，才可以抵消舵机延时带来的附加行驶路径。但并不是说只要将基准位置选得足够远就可以得到很大的入弯速度，答案是否定的。小车的转向为一个近似的圆周运动，不同的速度显然对应不同的行驶半径，即不同的路径。速度快时，半径大；速度慢时，半径小。过快的速度会使小车冲出赛道。竞赛赛道的弯道主要由360°、180°、90°、S型赛道组成。在图8所示的180°弯道中，中间的粗实线为引导线，最外围的实线为赛道边界，曲线1、2、3、4为小车行驶路线。设所有行驶路线有同样的入弯角度,曲线1、2、3为B点入弯，速度不同；曲线4为E点入弯，速度与曲线3速度一致。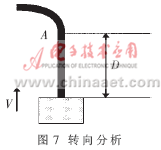

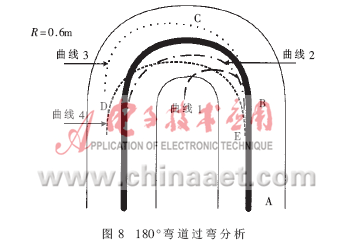
显然，曲线1、2、3中曲线3速度为最快，但路径却最长，同时还有冲出赛道的危险；曲线2虽"抄近道"，但速度稍慢；曲线1由于速度太慢而无法过弯。不难看出，其实曲线2、3、4的过弯时间相差并不是很大。但是由于曲线2中，由直道AB入弯时需要减速，过弯后需加速，这段时间却比曲线3、4来得长。经综合考虑，曲线3、4过弯时间最短。曲线3、4中曲线3很显然有冲出赛道的危险，因此曲线4为过180°弯的最优路径。可以看出，高速时提前入弯可以使小车以一个比较高的速度驶过弯道，同时保证了安全而又不会冲出赛道。

对于90°弯道，与180°类似，最优的策略是为保持直道高速行驶，通过上述的提前入弯策略保证安全过弯。

对于S道的进入，可以类推。而对于S道的行驶