发动机转速信号模拟器设计方案

平分20等份，通过不同占空比的PWM信号来逼近正弦信号中的20段，如图4(a)所示；把曲轴信号的一个正弦周期平分12等份，通过不同占空比的PWM信号来逼近其中的12段，如图4(b)所示。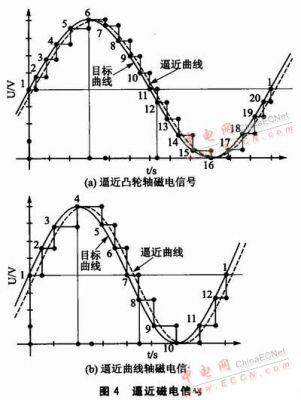

计算逼近各点时间间隔。计算公式如下：

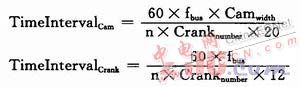
其中，TimeIntervalCrank为曲轴信号逼近各点时间的间隔计数值；TimeIntervalCam为凸轮轴信号逼近各点时间的间隔计数值；fbus为时钟总线频率(Hz)；Cranknumber为曲轴齿数(60、48)；Camwidth为凸轮轴齿宽(1，2，3…)；n为发动机目标转速(rpm)。

图4中，实线为逼近的目标曲线，虚线为逼近得到的曲线，逼近后的曲线相对于目标曲线向右平移了一小段相位，在程序中应提前逼近的开始时间，以消除逼近相位误差。

PWM通道的模数寄存器的值恒定为19，正弦信号最大值对应的值寄存器的值为Rang，如图4中的"6"点和"4"点。为了保证正弦信号的幅值随着转速值而变化，Rang随发动机转速增加而增大，

Rang=Rang(nspeed)。

当逼近一个曲轴信号正弦波时，正弦信号中各点对应的正弦值如表1所列。各点对应的单片机值寄存器的值为TPM2CV0=Rang(nspeed)×Sin(Number)。同理，可以得到逼近凸轮轴磁电信号20个点对应值寄存器的值TPM2CV1。

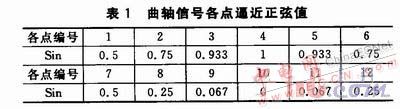
为了省去单片机做乘除法运算所占的时间，在程序中将各点对应的寄存器值做成数组，直接调用。如果要逼近与图4极性相反(先负后正)的正弦波，只需颠倒各点逼近顺序，即逼近顺序为20，19，18，…，2，1。

3．2 生成凸轮轴信号和曲轴信号

曲轴信号流程如图5所示。首先判断曲轴信号模式。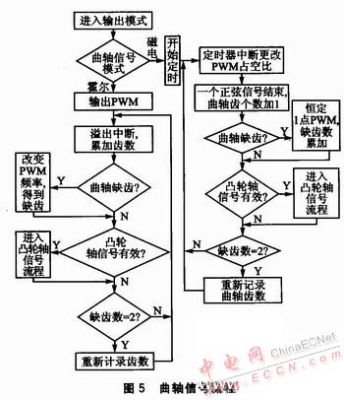

若模式为霍尔，则输出PWM霍尔信号。在溢出定时中断内累加曲轴齿数，若判断曲轴缺齿有效，则改变PWM频率，得到2个缺齿信号后，一个循环结束，曲轴齿数重新计数。在主程序中判断何时输出凸轮轴信号。

若模式为磁电，则输出PWM逼近信号，开始逼近定时。在定时中断中设置逼近各点的占空比，记录逼近点个数，一个正弦周期结束后，曲轴齿数累加1。若判断缺齿有效，则输出图4中恒定"1"点所对应占空比的PWM信号，两个缺齿后一个曲轴循环结束，曲轴齿数重新计数。在主程序中判断何时输出凸轮轴信号。

凸轮轴信号流程：若信号模式为霍尔，则在主程序中通过I／O口输出霍尔信号。若信号模式为磁电，则输出逼近PWM信号，在定时中断中设置逼近各点的占空比，记录逼近点个数，一个正弦周期结束后结束逼近定时，输出图4中恒定"1"点所对应占空比的PWM信号。

4 实验验证

设定模拟器参数如下：曲轴齿数为(60-2)个齿，凸轮轴齿数为(4+1)个齿，凸轮轴齿宽为6个曲轴齿宽，多齿超缺齿12℃A(曲轴转角是以℃A表示)，凸轮多齿超凸轮1齿为60℃A。通过示波器观察得到图6所示的信号。

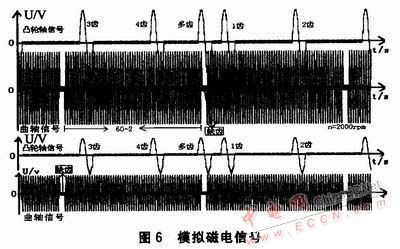
图6所示曲轴信号模式和凸轮轴信号模式均为磁电。模拟信号满足设定参数要求，并且幅值、相位准确，相对相位准确，频率稳定。上下两组信号的转速分别为2000rpm和1000 rpm。比较可知，磁电信号幅值随转速而变化。

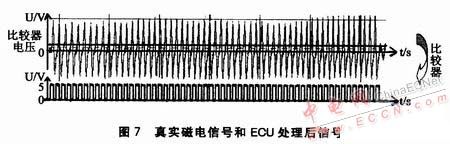
真实测得的磁电信号以及经ECU处理后的信号如图7所示。该信号在ECU中经过比较器处理后转换为方波信号，进而被单片机采集。模拟得到的磁电信号经过比较器后，同样转换为一个方波信号。虽然模拟信号与真实磁电信号存在差异，但是经过比较器后得到形同的方波信号，对单片机来说就是相同的信号，所以模拟信号能够替代真实的磁电信号。

5 结论

实验证明，PWM信号逼近正弦信号的方法可以在8位机上模拟出标准的磁电正弦信号，并且该信号可以替代真实的磁电信号。本模拟器系统可以在100～6000 rpm范围内精确模拟发动机转速信号，满足设计要求。由于8位单片机的处理能力有限，该模拟器不能实现磁电信号幅值随着转速连续、线性地变化，但是并不影响模拟器的功能。若改为使用。DSP处理器，采用级数逼近或者迭代逼近的方法即可实现。