高阶∑△ADC中的抽取滤波器的设计

近年来，∑△ADC在高分辨率、中低速应用场合，特别是高音质数字音频处理领域中的应用已经十分普遍。这种普遍应用得益于∑△ADC的特点：其中采用大规模数字电路作为抽取滤波器而降低对模拟电路的相关要求。∑△ADC由调制器和抽取滤波器组成。其中调制器决定了∑△ADC所能达到的精度，而抽取滤波器则决定了∑△ADC的面积和功耗[1]。因此设计合理的抽取滤波器不仅对ADC的整体性能有所提高，而且能够大量节省面积，减小功耗。

　　本设计的目标是16bit∑△ADC中的抽取滤波器，其中调制器的采样频率fS为2.8MHz，滤波器抽取比为64，通带截止频率为0.454fS，阻带截止频率为0.583fS，通带纹波为±0.05dB，阻带衰减为－65dB。

　　本文采用梳状滤波器与补偿滤波器级联的结构。若采用一级梳状滤波，主瓣和旁瓣的衰减最多达到13.5dB，根据设计指标，要达到65dB的衰减，采用五级级联结构就可以满足，最后加一级补偿滤波器进行降2抽取和通带补偿。这样就是六级64倍抽取滤波器。

1 梳状滤波器设计

　　梳状滤波器由于不需要乘法器而成为前级滤波的首选。其结构可以分为递归结构和非递归结构。递归结构因为前面级联的积分器工作频率为高采样频率，所以当抽取因子M和滤波器级数n比较大时就会带来非常大的功耗。同时，由于积分器部分为IIR滤波器，存在不稳定和溢出问题[2]。所以考虑采样非递归结构。它的传输函数推导为：

　　首先在时域写出抽取滤波器的输入输出的简单形式：

　　
　　滤波器将M个输入采样累加起来，然后除以M，得到输入的平均。
　　在Z域重写上式：

　　
　　可以用采样率依次降2的级联方法实现。这样每级传递函数展开为：

　　
　　可见，这是一个整系数的FIR滤波器，它只需要加法器和延时单元就可以实现。随着字长的增长，前级的滤波器虽然工作频率高，但字长短；后面的滤波器虽然字长长，但工作频率低，所以整体的功耗并不高[3]。通过将这种结构进一步改进，就得到了本设计中的滤波器结构。　　　　

　　由式(5)可见，改进后的前级滤波器字长进一步缩短，最后一级滤波器的字长增长一位。这样每级位数分别为4、8、12、17、24，直流增益为223，是上述标准结构增益的1/4。这样改的好处是高频工作的各级位数明显减少。位数的减少意味着加法器数量的减少，从而提高了速度，节省了面积。从图2的仿真结果看，改进滤波器结构的第一旁瓣与标准结构具有相当的衰减。只是在高频部分略有上升，但并不影响整体性能。

　　经过上面的分析，确定了合适的结构。现在考虑硬件实现，虽然上述结构不需要乘法器，但是需要加法器和寄存器来对数据作累加、延时和移位等操作。所以首先要选择合适的加法器和寄存器结构。在本设计中，考虑速度和功耗的要求，分别选择曼彻斯特进位链加法器结构[4]和C2MOS寄存器结构[5]。这是因为，曼彻斯特进位链加法器不仅速度快，而且它的和与进位输出具有近似的延时，总延时与级数具有线性关系。同时单级加法器只需要22个晶体管。而C2MOS寄存器属于动态存储器，它能在较高的工作频率下工作而不丢失数据。相对于静态存储器，结构简单，能够节省大量面积。

　　每级串行加法器的位数按照如下公式增长。其中Bin是每级的输入位数、Bout是每级的输出位数、N为各级的阶数、M为降采样比。
　　
　　首先利用加法器和寄存器反馈连接构成累加器，累加器的位数由上述公式给出。每级累加器的输入端都用一组与非门控制。当与非门的控制端为零时，重新开始累加。累加后用几组寄存器完成数据延时，再接多路选择器对数据进行移位，即乘上不同的整数倍数，然后输入到下一级的累加器中。依次类推。

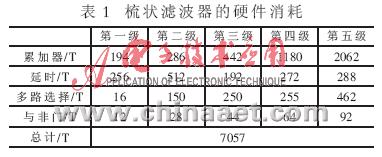
　　梳状滤波器的硬件结构如图1(a)，实现一级全加器需要22T（晶体管）、一位C2MOS寄存器需要8T，多路选择器和与非门控制则随位数而变化，总硬件消耗如表1。

2 补偿滤波器设计

　　梳状滤波器的最大缺陷就是通带衰减较大，不能满足整体滤波器通带纹波的要求。所以需要补偿滤波器对其进行补偿，以达到通带纹波的设计要求[6]。在本设计中，要求通带纹波为±0.05dB，即在信号带宽内，补偿滤波器的幅频响应与梳状滤波器的幅频响应的乘积应在±0.05dB之间。本设计中的补偿滤波器不仅要对通带补偿，而且还要实现采样率降2和增大阻带衰减的功能。利用Matlab 7.0的Filter design &analysis tool工具进行设计，因为FIR滤波器具有线性相位并且系数对称，所以最终确定的补偿滤波器为52阶FIR滤波器，总共有26个系数。理想FIR滤波器的系数为无限长，经过截断和优化后，各系数如表2。