去高斯段法快速求解运动检测自适应门限算法

1 引? 言

由于受到应用环境和噪声的影响,不同的图像序列包含不同的图像分量,而且它们的变量特性也明显不同,所以对于运动检测,任何预设的固定门限值都是不合适的。于是出现了求解自适应门限问题，同时自适应门限的求解也增加了数据的运算量。

相关文献提出了两类解决方法：(1)采用学习和训练的方法来估计背景分布,根据像素点是否服从背景分布来进行运动检测【1~2】。此类方法在一定程度上实现了门限的自适应选取,但是通常需要假设背景像素点服从某一特定的分布函数,并且计算量偏大。(2)灰度直方图熵门限方法【3~5】。该类方法对帧差绝对值建立一维或二维直方图,并运用熵准则求解全局门限,但是实验表明,如果目标和背景的对比度偏低,采用该类方法得到的门限进行运动目标提取会产生很大误差。

针对上述问题，充分利用差分图各等级灰度的统计特性，提出了新的运动检测自适应门限快速求解算法。同时进行了实验，统计了实验数据。

2 理论基础

图像包含各种各样的噪声,这些噪声可能在传输中产生,也可能在量化等处理中产生。噪声产生的原因决定了它的分布特性及它和图像信号的关系。一般情况下,由视频镜头产生的噪声,以及视频序列中的随机噪声、亮度变化、背景纹理的变化等统计量噪声都服从均值为零的高斯正态分布,而由运动物体引起的亮度变化与噪声的分布是独立的。文献【6】也指出视频图像中的噪声具有高斯特性。

因此，可以认定差分图中的噪声服从某种特性的高斯分布，并且该高斯分布的均值的期望为零。因为差分图的绝对值特性，差分图中的噪声在直方图上呈现的是高斯曲线的右边部分。并且随着信噪比的降低而更加明显。

3 仿真验证

下面用MATLAB对上述分析进行验证，被验证图像选取如下

对差分图1(c)建立直方图，其灰度范围为：0~162，164~166，170，171，175，178，179，181，共172个灰度等级。为增加可视化，将差分图分为三段呈现如下。

由图2可知，在灰度值为0~15范围内，直方图呈现的是高斯曲线的右边部分。根据前一段论述，可以确定门限为15。效果如下所示。

结合以上分析，可以确定此方法是可行、有效的。

4 算法设计

算法的核心为如何在直方图左端最大范围地确定高斯曲线部分。首先，需要确定高斯分布的均值 ，因为噪声分布的均值的期望为零，所以高斯分布的均值分布在直方图的左端，并且其数量 具有局部极大值的特点。即：

其中表示图2中 的前一个和后一个灰度值，不是绝对的减一，加一动作。根据式子（1），按如下步骤求得高斯均值 。

根据高斯分布在均值右边单调下降的特点，按如下步骤确定高斯曲线段最大范围，从而得到最佳自适应门限 。

其中表示图2中 的右一、右二灰度值，不是绝对的加一，加二动作。也即，在相邻三个灰度值的数量上不体现递减特性时界定高斯曲线终止。

5 实验结果与分析

测试环境：Intel(R) Pentium(R) D CPU 3.40GHz,VC++6.0。测试序列为：国际标准测试序列hall_objects，和自制序列01，02，03，04。其中统计时间包含：差分图计算时间和门限求解时间。

表1 各图像序列门限求解时间

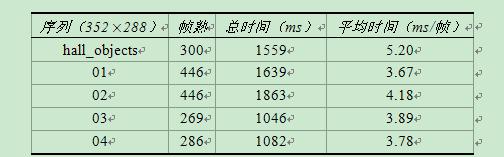
测试结果如下：

图4 hall_objects实验结果图5 序列01~04实验结果

图5 序列01~04实验结果

从实验结果可知，本算法运算速度快，门限能够很好保留运动目标轮廓。

6 结语

将差分图看做噪声和运动目标两部分，着眼于通过去噪达到运动目标提取的目的。根据差分图中噪声分布的高斯特性，在直方图中进行高斯段界定达到自适应门限求解。从而大大降低了计算量，通过实验证明，本算法具有快速、准确的良好性能，并具有一定的消除阴影能力，非常适合实时处理，具有很好的实用价值。