矢量调制分析基础

更深入地了解这些误差信号的本质与来源。频率峰值通常会对应方框图中某处的一个信号。I-Q 幅度误差( 轨迹C) 和I-Q 相位误差( 显示D) 显示了I-Q 测量信号和I-Q 参考信号间的误差。I-Q 幅度误差显示幅度误差，I-Q相位误差显示相位误差。

图13. 轨迹A ( 误差矢量时间) 显示了符号点处的误差矢量幅度。轨迹B ( 误差矢量频谱) 显示了误差矢量时间数据的频谱。轨迹C (IQ 幅度误差) 是测量IQ 波形和IQ 参考波形的幅度差。

轨迹D (IQ 相位误差) 是测量IQ 波形和IQ 参考波形的相位差。

符号表/ 误差汇总

符号表/ 误差汇总测量结果可能是数字解调最强大的工具了。你可以看到解调比特，以及所有解调符号的误差统计。例如，查看rms EVM 值可以帮助你快速评估调制精度。还有其它很多有价值的误差报告。图14 显示了前面使用的QPSK 信号的符号表/ 误差汇总数据。标记读数显示的是符号表中突出显示的比特对应的值，代表符号3，数值为2 ("10"的二进制值)。可以看出这个值与QPSK 调制所需的双比特码元一致。误差表显示了适用于QPSK 调制信号的统计数据与误差数据。其它误差值为其它格式所用。我们已经讨论了一些基本的调制测量，但还有很多定性显示和定量测量并未涉及。

图14. 符号表/ 误差汇总数据提供解调比特及所有已解调信息的误差统计。

模拟调制分析

矢量调制分析可以提供的另一种重要的测量工具是模拟调制分析。模拟调制产生AM、FM 和PM 解调结果，类似于调制分析的输出，允许你查看幅度、频率和相位特性对时间的关系。这些模拟调制分析能力增强了VSA 已有的数字调制分析功能，提供完整的分析数字通信系统的测量解决方案。例如，可使用模拟调制能力分析像FSK ( 频移键控) 这样的有意调制; 像相位噪声或AM-PM 转换这样的无意调制; 或者像频率或相位稳定或脉冲成形过程这种单脉冲信号参数。

解调信号的过程看上去挺复杂，但矢量调制和I-Q 调制过程的基础特性使得解调变得简单。前面提到的矢量或IQ 图( 图2 和11) 显示了调制载波相对未调制载波的瞬时幅度和相位，这有助于显示数字调制特性。不过它还提供了一个简单的方法来查看模拟调制信号特性，例如图15 所示的AM、PM 和FM 调制。未调制连续波(CW) 信号简单地显示为一个幅度与相位恒定的固定点。AM 信号的轨迹经过原点沿着固定线路，只有信号幅度发生改变。FM 信号的轨迹是以原点为中心的圆圈，瞬时频率偏差由相位变化率给出。PM 与FM 的轨迹类似，当然，相位的相对变化是关键参数。在矢量调制中，幅度和相位可同时改变，矢量轨迹会在幅度和相位上都发生变化。

图15. I-Q 示意图中I-Q 平面上的模拟调制特性。

传统上，为了查看载波调制波形( 调制包络)，应当通过检波移除载波并将结果波形显示在幅度对时间的示波器上。不过，取代在载波上检测调制的思想，在矢量调制中，我们将载波"搬移"或"下变频"到0 Hz 之后再在剩下的部分里查看调制。频移的直观图将显示利用基本三角恒等式载波上幅度和相位变化是如何被"检测"的。

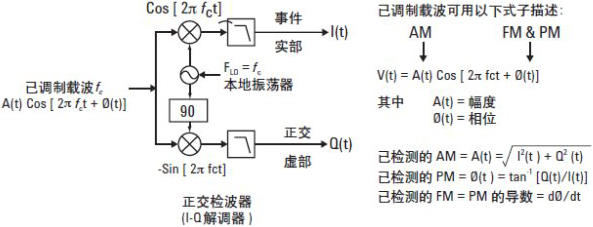
图16. 调制通过搬移载波频率(fc) 至0 Hz 测量。当数字LO 频率等于调制载波频率时，正交检波器的输出 —I(t) 和Q(t) 时域波形 — 就是载波上的调制。

如图16 所示，复调制载波信号以(V(t) = A(t)Cos[2πfct + Ø(t)]) 表示，频率fc 是用于频率转换的正交混频器( 或正交检测器) 的输入。为恢复基带调制信号，首先通过设置LO 频率为fc 将载波下变频至基带(0 Hz)。随后基带信号经过低通滤波，只留下差频。这个过程生成实部I(t) 和虚部Q(t) 时域波形，表示已调制载波信号与未调制LO 信号的幅度和相位差，以载波为参考。这是载波调制以I(t) 和Q(t) 分量( 直角坐标) 表示的形式，而不是幅度A(t) 和相位Ø(t)。前面提到I-Q 解调执行极坐标—直角坐标的转换。不过，通过对I(t) 和Q(t) 分量应用一些运算和简单的三角恒等式，我们也能够获得瞬时幅度A(t) 或相位Ø(t) 这些载波上的变化。这就是AM 和PM 调制。

幅度调制AM 是载波幅度A(t) 随时间的变化，由I(t) 和Q(t) 的平方和开平方根得出。

AM = A(t) = sqrt[I2(t) + Q2(t)]

相位调制PM 是相位Ø(t) 随时间的变化，等于[Q(t)/I(t)] 的反正切。频率调制FM 是相移对时间dØ/dt 的导数。即，FM 是PM 的导数:

从I(t) 和Q(t) 开始，通过应用基本三角恒等式，我们完成了载波的第一阶解调，能够查看AM、PM 和FM 调制。实际中，VSA 软件使用精密的解调算法再结合频率和相位误