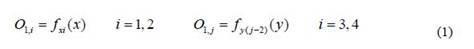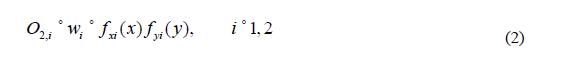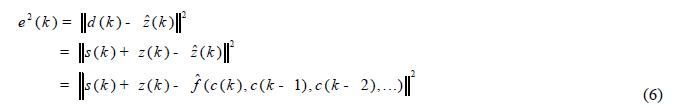基于ANFIS 的有色噪声抵消技术
时间:04-21
来源:EDN
点击:
0 引言
在信号检测中通常会遇到信号淹没在噪声中,当这种噪声为高斯白噪声时,可以采用线性滤波的方法,自适应噪声抵消(adaptive noise cANCeling,简称ANC)方法首先由Widrow 和Glove 提出[3],使用线性滤波器的ANC 系统已成功地应用于心电图、电话回声消除、电话干扰消除等实际问题,但对于噪声具有非线性传播性质时,使用线性滤波效果往往很差,甚至根本起不到抑制噪声的作用。
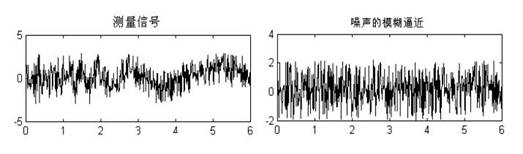
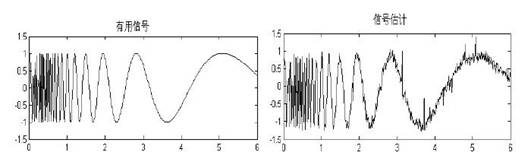
有色噪声可看作是白噪声经过非线性动态处理后产生的,所能得到的是有用信号与有色噪声的混合噪声源分量。信号滤波的目标是消除噪声,提取有用信号。这里利用自适应神经模糊推理系统ANFIS 对非线性动态特性进行建模,并利用ANFIS 逼近有色噪声,然后从测量信号中消除有色噪声得到有用信号。可见,ANFIS 可用作非线性滤波器。
1 ANFIS 网络的结构
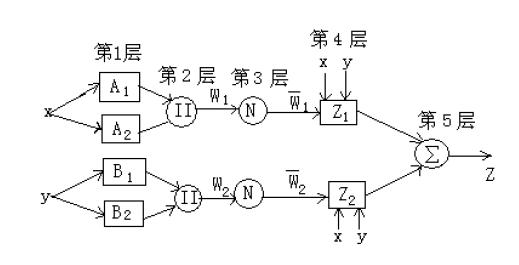
1985 年Takagi 和Sugeno 提出了一种非线性T-S 模糊模型,即后来的Sugeno 模糊模型,是一种对有精确输入、输出数据集产生模糊规则推理的系统化方法。它结合模糊逻辑与神经网络二者之优势,改善了传统模糊控制设计中必须人为地不断调整隶属度函数以减小误差的不足,采用混合学习算法调整前提参数和结论参数,自动产生模糊规则。后来,Tang Roger 提出与一阶Sugeno 模糊模型功能等同的基于自适应神经网络的模糊推理系统(ANFIS ) 用来实现Sugeno 模糊模型的学习过程。ANFIS 可以认为是Sugeno 型模糊模型的神经网络实现,该网络是一个多层前馈网络,结构如图1。
在信号检测中通常会遇到信号淹没在噪声中,当这种噪声为高斯白噪声时,可以采用线性滤波的方法,自适应噪声抵消(adaptive noise cANCeling,简称ANC)方法首先由Widrow 和Glove 提出[3],使用线性滤波器的ANC 系统已成功地应用于心电图、电话回声消除、电话干扰消除等实际问题,但对于噪声具有非线性传播性质时,使用线性滤波效果往往很差,甚至根本起不到抑制噪声的作用。
有色噪声可看作是白噪声经过非线性动态处理后产生的,所能得到的是有用信号与有色噪声的混合噪声源分量。信号滤波的目标是消除噪声,提取有用信号。这里利用自适应神经模糊推理系统ANFIS 对非线性动态特性进行建模,并利用ANFIS 逼近有色噪声,然后从测量信号中消除有色噪声得到有用信号。可见,ANFIS 可用作非线性滤波器。
1 ANFIS 网络的结构
1985 年Takagi 和Sugeno 提出了一种非线性T-S 模糊模型,即后来的Sugeno 模糊模型,是一种对有精确输入、输出数据集产生模糊规则推理的系统化方法。它结合模糊逻辑与神经网络二者之优势,改善了传统模糊控制设计中必须人为地不断调整隶属度函数以减小误差的不足,采用混合学习算法调整前提参数和结论参数,自动产生模糊规则。后来,Tang Roger 提出与一阶Sugeno 模糊模型功能等同的基于自适应神经网络的模糊推理系统(ANFIS ) 用来实现Sugeno 模糊模型的学习过程。ANFIS 可以认为是Sugeno 型模糊模型的神经网络实现,该网络是一个多层前馈网络,结构如图1。
|
图1 Sugeno 模糊系统等效的ANFIS 网络 假定模糊规则库包含两种规则: Rule1: if x is A1 and y is B1, then z1=p1x+q1y+r1 Rule2: if x is A2 and y is B2, then z2=p2x+q2y+r2 网络共有5 层,各层功能如下:第1 层:Ai 和Bi 为输入变量的模糊子集,该层节点的激活函数代表模糊变量的隶属函数,该层的输出代表模糊化结果,即隶属度,其中一个节点的传递函数可以表示为
第2 层:将模糊化得到的隶属度两两相乘,该层的输出代表着模糊规则的强度或适用度。
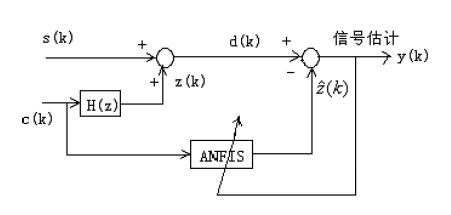
(1)获取样本数据和检验数据; (2)确定输入变量的隶属函数的类型和个数; (3)由genfis1 函数确定ANFIS 的初始结构; (4) 利用anfis 函数训练ANFIS, (5) 检验得到的ANFIS 的性能。 2 利用ANFIS 网络噪声抵消原理图
|
- 芯海科技推出有效精度高达23.5位的ADC芯片CS1232 (04-02)
- Avago推出四款低噪声放大器(04-23)
- 安森美推出集成ESD保护的共模滤波器(05-26)
- Avago推出高功率开关低噪声放大器模块(06-02)
- TI推出隔离式 DC/DC 转换器TPS55010(06-10)
- 村田推出DE6系列KJ型安规陶瓷电容器(06-24)