RF circuit Stability analysis by Transfer function
I have a question about stability analysis of RF circuit by transfer function. Let's say I derive transfer function of a circuit and get:
H(s)=N(s)/D(s)
D(s) = a*s^2+b*s+c where a, b, c are function of 2 parameters x & y.
N(s) is also quadratic function of s. I think I can neglect N(s) because I just focus on stability.
I will find roots of D(s)=0 are: s1 & s2. Of course, s1 & s2 depend on x & y and may be complex number. To estimate the stability of circuit, I use MATHLAB to plot s1 & s2 on complex plane (variables are x & y). If real(s1) or real(s2) is positive, the circuit will oscillate at those specific x0 & y0.
Am I right? Please help me. Every comment is appreciated.
If Real(s1) and Real (s2) is positive, the circuit will absolutely be unstable regarding to Hurwitz criteria.
In microwave technique, we can test the unconditional stability of circuit by Mu standard
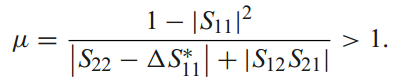
If Mu > 1, does it mean that there are no pole on right-half complex frequency plane?
This is valid single stage systems only.If stage number N>2 the equation is not valid anymore at least theoretically.
In this case, NDF ( Normalized Determinant Function ) can be examined but it's not so easy.
http://www.reveyrand.fr/publications/64.pdf
Thank BigBoss.
I have question: Assume I have a two port network and its transfer function. Can I use Mu-standard to check its stability? If not, the Mu-standard should not be employed for a complex two port network?
Sure, K Rolett stability factor and Mu stability factor should be examined.But Input and Output Stability Circles should also be carefully checked up to fmax to avoid unwanted oscillations.
But if you circuit has N>2, while overall the circuit is seeming stable an oscillation may appear between interstages, take care of it..
To analyse the stability of circuit, sometimes it is difficult to derive S parameters and calculate K or Mu factor. So derive the transfer function and calculate the poles may be better.
Does anyone know other methods? Please give me advice. Thank.
