Matching (maximum power transfer), NF
I understanding Frie's equation, maximum power theorem etc for a conventional receiver. However, do I understand it right that all this is based on the fact that we assume a given input power?
Suppose I can pick the power level of my input signal arbitrarily (only limited by linearity/swing) and after the ADC I want a certain end-to-end SNR of say -45 dB. Would the NF in this case matter at all?
(Reason: My signal is actually a transmitter output and hence 40-50dBm, hence I even need to atternuate it to make it compatible with my receiver)
1.) An ADC is known for its horrible NF, say 30dB. A conventional receiver would add LNA & gain in order make the overall NF much lower (through Frii's), say 5 dB. However, these gain stages add noise themselves. So if I assume the maximum input swing of my ADC is 2Vpp (13 dBm) and I can pick my input power level of the receiver arbitarily, is there any way to beat connecting the ADC straight to the source, despite having a high NF of 30 dB?
2.) What is the actual reason I want to match? Yes, for maximum power transfer ... but the actual reason? Say, the source has a conventional 50 Ohm source resistance and I design my receiver with, say Rin=1k. Then the noise power at the input of the receiver would be 4kT50(1000/(50+1000))^2 1/1000 ~ 4kT50/1000 ... 250x smaller than with matching and ... since I can choose the power at the input anyway ... it would not matter.
3.) Some numbers: As indicated, I need end-to-end SNR of 45 dB and I have 800 MHz. So the total integrated noise floor alone is -85 dBm. So I have "SNR = 45 = Pin + 85 - NF". Combining I get "Pin = -40 + NF. Assuming the 30dB NF ADC as mentioned above, this would be Pin >= -10 dBm! Pretty high number, specifically for 1VDD technologies where the maximum swing is maybe 500mV and hence 7 dBm.
3.a.) Same as question 1) but with numbers: Is there anything I can do to improve the SNR (e.g. picking a lower Pin but some amplification)?
3.b.) I want to do some analog system signal processing before the ADC, speficially mixing and integrating. Now I could set the unity-crossover frequency of the integrator to the bandwidth, 800 MHz and add enough gain to do the integration. But I could also set the unity crossover frequency much lower and use a high input power instead. In that case, there would be a passive RC (and low gain) in front of the ADC (which would attenuate) the signal. However, I can pick it as high as permitted by the input/output swings (~7dBm). Is there any way to beat this scenario by adding gain stages or can I say it's always best to do the least work if the input power can be chosen arbitrarily?
I can not understand what you mean by "source" at all.
If amplitude level of source is enough large comparable to FullScale of ADC, you can connect it to ADC directly.
Don't consider NF.
Consider input referenced noise voltage at ADC input.
About your questions 2), 3), 3a) and 3b), describe more clearly.
It is very difficult to find out what is your main question.
I agree, your overarching question is confusing. From the title and your first comments, perhaps you are asking the difference for maximum power transfer in the far-field and near-field case?
Ok, thanks for your answers, I'll try it again.
Signal source (modeled as voltage source) with 50 ohm in series
ok, thanks
I think there are many issues in my understanding: With matching, I do understand that it results in maximum power transfer ... but maybe not why exactly.
What does that mean in practice for a circuit? Does it just mean that the amount of energy transferred is lower (or there is a certain signal attenuation) or can I expect distortion (due to reflections) or other side effects if I do not match?
I mean, for a transmitter I do understand I want to deliver the maximum power because that's just required for a certain distance. But for a receiver, I am interested in the information anyway, so wouldn't it be better if I just look at the voltage?
The classical example: Signal source (voltage), Rs ohm in series and Rin of my receiver. Suppose I make Rin=1G. Then the efficiency would be 100%. I would not deliver power into the receiver but why would I care as long as the amplifier senses the right voltage?
Furthermore, with arbitrary Rs & Rin, the signal and noise power is given as (is this correct?):
Psig = Vsource^2(Rin/(Rs+Rin))^2/Rin
Pnoise = 4kT*Rs(Rin/(Rs+Rin))^2/Rin
The SNR Psig/Pnoise stays constant regardless of Rin & Rs if I take Vsource as the actual signal source.
However, as I described in my initial posting, my receiver senses a 50 dBm signal which must be attenuated anyway so it has maybe 100mVrms (-7dBm @ 50 Ohm). To my understanding, I do not use "Vsource" here but look at the input node of the receiver to have a certain power level Pin. For example, I would use a power meter and adjust the attenuator until I get the desired Psig.
On the other hand, Pnoise becomes smaller, the larger Rin (larger mismatch). So again, by making Rin=1G I can effectively eliminate the source noise while I can leave the signal level unchanged. Do I miss something?
See the followings.
https://www.edaboard.com/thread347861-2.html#21
https://www.edaboard.com/thread347861-2.html#28
This can never be true for RF.
If Rin is high such as 1Gohm, parasitic capacitance Cin can never be ignored.
Right.
I can not understand what you want to mean at all.
Psig/Pnoise=Vsource^2/(4kT*Rs) is dependent on both Vsource and Rs.
I can not understand what you want to mean at all.
Contribution of Vsource^2 and 4kT*Rs by Rin are same.
Again, I can not understand what you want to mean at all.
SNR of signal source is constant regardless of input impedance of DUT, Rin.
Sure, this is just an example. Say it can be 1k or 10k. Then it is still close to 100%. I just want to understand if there is a problem if I just maximize Rin (or |Zin| for that matter).
I can not understand what you want to mean at all.
Psig/Pnoise=Vsource^2/(4kT*Rs) is dependent on both Vsource and Rs.
So again: I have a receiver with a LARGE input signal that I even need to attenuate to make it something like 100mVrms in voltage amplitude (to meet the swing requirements)
I want to maximize SNR.
I want to know if I need to set Rin to 50 Ohm (as the source resistance) and what the implications are if I do not.
My claim is that I do not care about the voltage of "Vsource" but at the voltage right in front of the receiver (between Rs and Rin), let's call this node Vx.
Since my signal is large I can just dial the knob of an attenuator until I get Vx where I want it, say 100mVrms. So this number is fixed and does not depend on any quantity.
Then I want to maximize SNR, i.e. minimize the noise voltage which is given as 4kT*Rs(Rin/(50+Rin))^2. If Rin=50, this is kT50. If Rin=10k, this is ~kT200 - a factor of 4 worse. Contrary to what I said before, the best SNR would not be if Rin is large but if Rin approaches zero. Is this true? That would be bad news.
The reason why I was getting confused before was that I thought I can adjust the input power arbitrarily too. But this is not true: If I am limited by the input voltage swing, the maximum input power directly depends on Rin, the same way as for the noise and hence SNR is the same.
Let me also bring up again something from before which would probably really solve my confusion:
So why do we care about maximum power transfer (and hence matching) in a receiver? If Rin=infinity, the receiver would just sense the voltage (at the gate of a MOSFET e.g.) while not drawing any power at all (maximially efficient).
I think it would be helpful to look at the parameters of real receivers.
Not all receivers are using impedance matching. Receivers up to SW usually don't. Respectively, there noise performance can't be usefully described by a noise figure, instead an input noise voltage (for a given receiver bandwidth) is often specified.
Your initial post seems to refer to UHF range, here receivers have 50 or 75 ohms input impedance and a NF number. Amplifier transistors have considerable real input impedance for UHF, impedance matching is feasible and recommended for best SNR.
The bottom line is you're ultimately constrained by the SNR of the ADC. Thinking about things in terms of NF is more appropriate when your source noise is dominated by thermal noise.
Recall that NF is defined as the SNRin-SNRout. For a high power source, the SNRin can, in principle, be extremely high if you assume its noise is just the thermal noise of its source impedance (so a 50dBm source would still have -174dBm/rt(Hz) of noise). Obviously no ADC is going to be able to digitize such a huge dynamic range, regardless of what circuitry you put in front of it. But this is usually a moot point, since the noise from high power source is never going to be -174dBm, since it's being generated using a real, noisy amplifier whose output noise will be far above -174dBm.
Your confusion is no more than your lacking of understanding simple math.
Reconsider simple math befire posting.
SNR is constant regardless of Rin value.
Again surely see the followings.
https://www.edaboard.com/thread347861-2.html#21
https://www.edaboard.com/thread347861-2.html#28
Wrong. SNR is constant regardless of Rin value.
No. If Rin=0, both signal and noise voltage at node x are zero.
If Rin=0, you have to define SNR by current instead of voltage.
Here SNR is constant even if Rin=0.
Consider available power of signal source.
Available power of signal is Vsource^2/(4*Rs)
Available power of noise is k*T
SNR defined by ratio of available power is Vsource^2/(4*k*T*Rs).
This is coincident to your Psig/Pnoise, although I don't refer Rin at all.
Again, SNR of signal source is constant regardless of input impedance of DUT, Rin.
Again surely see the followings.
https://www.edaboard.com/thread347861-2.html#21
https://www.edaboard.com/thread347861-2.html#28
See the followings.
http://www.designers-guide.org/Forum...1065493598/1#1
http://www.designers-guide.org/Forum...1195659245/5#5
Ok, thank you. As others indicated in that topic ... it's also the first time for me that I hear this distinction.
But it makes sense.
So having \Gamma_V \neq 0 implies linear distortion. From a system level perspective: The action of this mismatch can be described by a linear filter, so hence I could use a digital filter (operating at the baseband samples of the signal that's transmitted) to account for those effects, is this true?
I think we are still talking about something different.
As I indicated above I do understand that SNR is independent of Rin if the signal source is considered Vsource. Because then Vsource and 4kTBRs have the same voltage divider.
Maybe a picture helps to clarify:
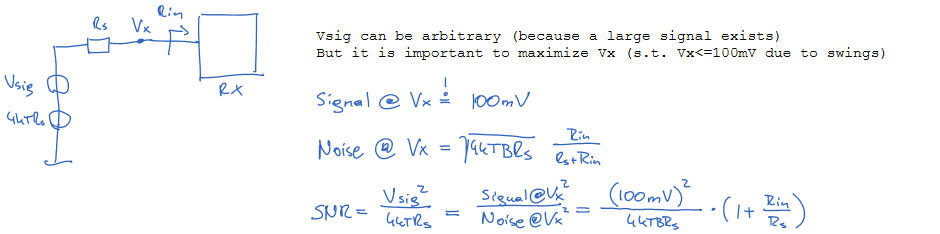
Here I want to fix the signal at Vx to something, say 100mV while minimizing the noise. Yes, the SNR stays constant regardless of Rin; it also implies that Vsource is much larger.
And I think I see the caveat already: While I can indeed have Rin -> 0 for best SNR in this case, it also implies that the voltage Vsource becomes huge and there are probably limits as well ...
See the followings.
http://www.designers-guide.org/Forum...1065493598/1#1
http://www.designers-guide.org/Forum...1195659245/5#5
