Why does series inductor at GPS LNA input improve sensitivity?
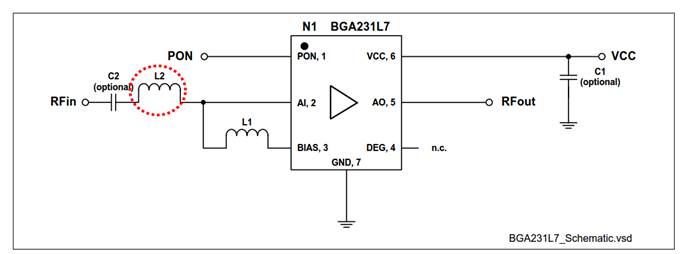
ALM-2412 of AVAGO
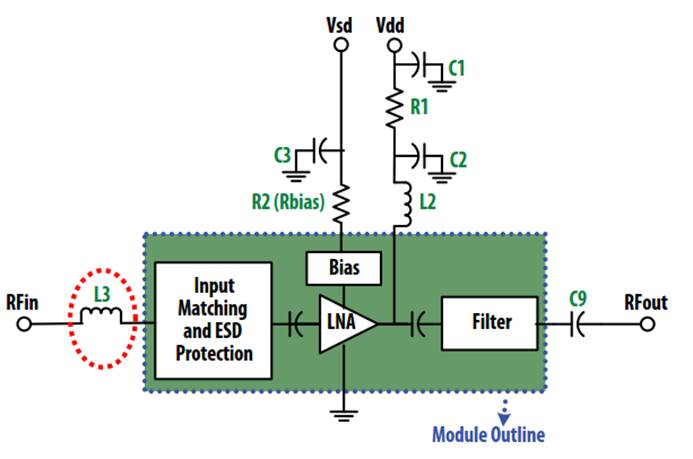
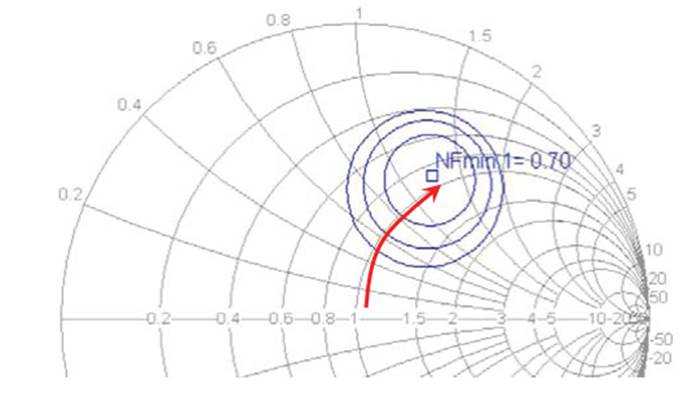
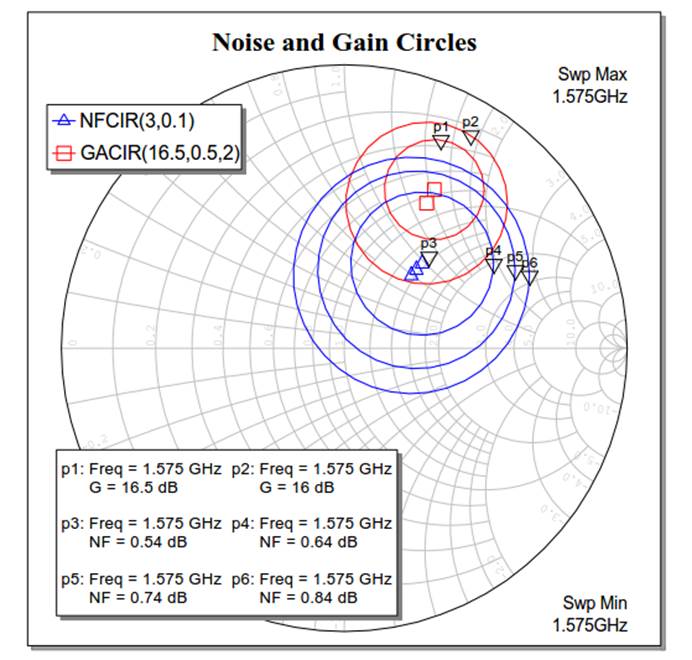
As shown above, obviously, the series inductor at LNA input is Input Matching to achieve minimum noise figure, thereby improving sensitivity.
Nevertheless, the inductor value is 6.8nH and has 1.8dB insertion loss@ GPS frequency.

That?s to say,

The inductor can increase insertion loss 1.8dB and reduce noise figure simultaneously.
Therefore, there will be 3 possible situations:
1. Noise figure reduces more than 1.8dB : The sensitivity improves.
2. Noise figure just reduces 1.8dB : The sensitivity remains the same.
3. Noise figure reduces less than 1.8dB : The sensitivity aggravates.
But, according to my previous experience, the sensitivity always improves.
So, I?m confused.
Does the series inductor always reduce noise figure more than its insertion loss ?
If not, why does the inductor be still able to improve sensitivity ?
Thanks a lot~!
I think the 1.8dB insertion loss is only true for 50 Ohm source and 50 Ohm load, where the series L causes mismatch. But here, where the L is added for a good reason, only losses (dissipation) from the inductor's series resistance would cause us trouble.
Why do you think that 6.8nH series inductor will increase the "Insertion Loss" ? OK, there will be a small insertion loss due to this inductor but not 1.8dB.
I believe you have confused Insertion Loss and Gain Reduction because of Noise Matching and Gav Matching.The difference can be 1.8dB between Noise Matching and Gav Matching but it doesn't mean the 1.8dB will be inserted between input and LNA.
Hi,
Thanks for your reply. My thought is as below:
1. According to Friis formula :
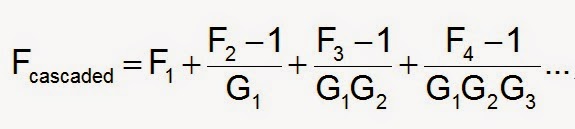
For the total noise figure of RX path,
the individual noise figure of these stages posterior to LNA can be ignored because they have gain in their denominator.
For example :

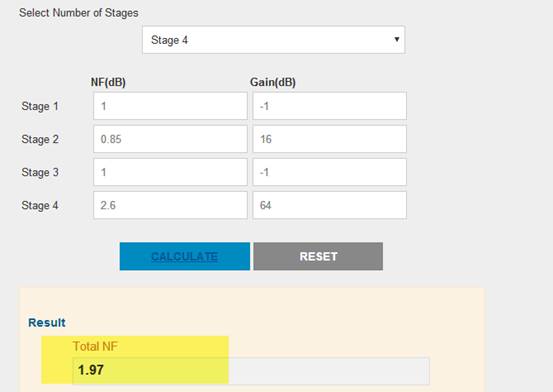
The RX path has 4 stages
Stage1 : NF = 1dB, Gain = -1 dB
Stage2 : NF = 0.85dB, Gain = 16 dB
Stage3 : NF = 1dB, Gain = -1 dB
Stage4 : NF = 2.6dB, Gain = 64 dB
Thus, its RX path total noise figure = 1.97(dB)
Nevertheless, if we just add the noise figure of stage1 and stage2 together:
1dB + 0.85dB = 1.85 dB
The result approximates the previous calculation (1.97dB)
Thus, if the gain of LNA is large enough,
RX path total noise figure = total insertion loss prior to LNA + LNA noise figure
As for your question:
Why do you think that 6.8nH series inductor will increase the "Insertion Loss" ?
1. Due to the character of the 6.8nH inductor itself, it has about 1.9 dB insertion loss@ GPS frequency(1575 MHz).
Ideal Model Simulation : 1.679 dB
Actual Model Measurement : 1.962 dB

2. Because the series inductor is at LNA input,

As mentioned above,
RX path total noise figure = total insertion loss prior to LNA + LNA noise figure
Thus, its 1.9dB insertion loss increases RX path total noise figure 1.9dB as well.
3. Indeed, the series inductor can reduce the noise figure of LNA.
Again, as mentioned above,
RX path total noise figure = total insertion loss prior to LNA + LNA noise figure
Thus, RX path total noise figure reduces as well.
4. According to point2 and point3, we know that the series inductor can increase and reduce RX path total noise figure simultaneously.

As a result, if sensitivity improves,
the noise figure of LNA must reduce more than the insertion loss of the series inductor at LNA input.
For example:
Insertion loss = 1.9dB, LNA noise figure reduces 2dB => Sensitivity improves 0.1dB
(1.9 ? 2 = -0.1, it means that total noise figure reduces 0.1dB)
Otherwise, the sensitivity degrades.
For example:
Insertion loss = 1.9dB, LNA noise figure reduces 1dB => Sensitivity degrades 0.9dB
(1.9 ? 1 = 0.9, it means that total noise figure increases 0.9dB)
Is my thought incorrect?
If yes, what?s the blind spot?
Thanks a lot~!
How can you claim 1.8 dB insertion loss caused by the series inductor without ever referring to LNA input impedance respectively S11?
According to my RF noise analysis textbook, this "noise figure = insertion loss" passive device math is only valid if the 2-port is matched at both input and output.
Dear Critereon456,
You confuse "Mismatch Loss" and "Insertion Loss".
The loss which is coming from the inductor above is a "Mismatch Loss" due to mismatching between the ports due to inserted coil between the ports.Because Input Impedance that is seen from a port is different than system characteristic impedance and of course there is a reflection, so if the energy is reflected, there will absolutely a loss.
An ideal coil ( zero internal resistor) never contributes into noise of a system even its value is gigahenry..
The non-ideal coils have a small series resistance and only this resistance contributes into Noise Figure of a system.Therefore you confuse two losses.
Thanks your detailed reply.
I know what the blind spot is.
