What is the reason for minor lobes being formed in a directional pattern?
If you read an antenna theory text book and study how directional patterns are created (by superimposing the characteristic of multiple elementary antenna elements), you see that they are hard to avoid.
That is a bit like asking Why is there air. Minor lobes are a natural occurrence of practical distributions. There are strong correlations to Fourier transforms. A binomial aperture distribution does not form minor lobes but it is relatively impractical to produce. High gain/directivity arrays actually produce the highest gain when sidelobes are present. Reducing sidelobes actually generally spreads the main beam and thus usually degrades peak performance. Phase and amplitude disturbances in an aperture generally also lead to the appearance of minor lobes. The other thing that minor lobes do is give antenna engineers something interesting to do.
Simple array antenna feeding network provides equal phase delays from each element to a common antenna port. Let's put some signal source in front of antenna. In this case each antenna element will receive signal with almost equal phases and amplitudes, thus each individual signals will sum up to a maximum possible amplitude. If we start to move signal source away from initial position, then each array antenna element start to receive the same signal, but with shifted phase. If relative phase shift between received signals become close to +-180 degrees, then it is almost cancelled out. Minor lobes appear because significant part of antenna element phases are not cancelled out.
Basic understanding of side lobe phenomenon does not require any knowledge about antennas. You only must know that each antenna element have some position in space, and that received signal phase may be calculated based on that position and incoming/outgoing signal direction using Array Factor formulas (considering only reciprocal antennas). Here is an example I made some time ago to learn Array Factor:
F(theta,phi,x,y)=Exp(i*2*Pi*x*Sin(theta)*Cos(phi)) *Exp(i*2*Pi*y*Sin(theta)*Sin(phi)); fld(t,p,dx,dy)=F(t,p,0*dx,0)+F(t,p,1*dx,0)+F(t,p,2*dx,0)+F(t,p,3*dx,0) +F(t,p,4*dx,0)+F(t,p,5*dx,0)+F(t,p,6*dx,0)+F(t,p,7*dx,0) +F(t,p,8*dx,0)+F(t,p,9*dx,0)+F(t,p,10*dx,0)+F(t,p,11*dx,0) +F(t,p,12*dx,0)+F(t,p,13*dx,0);
This formulas describe antenna consisting of 14 elements (n=0 to 13). DX is spacing between elements. For example, it may be patch array antenna with single row of 14 patches.
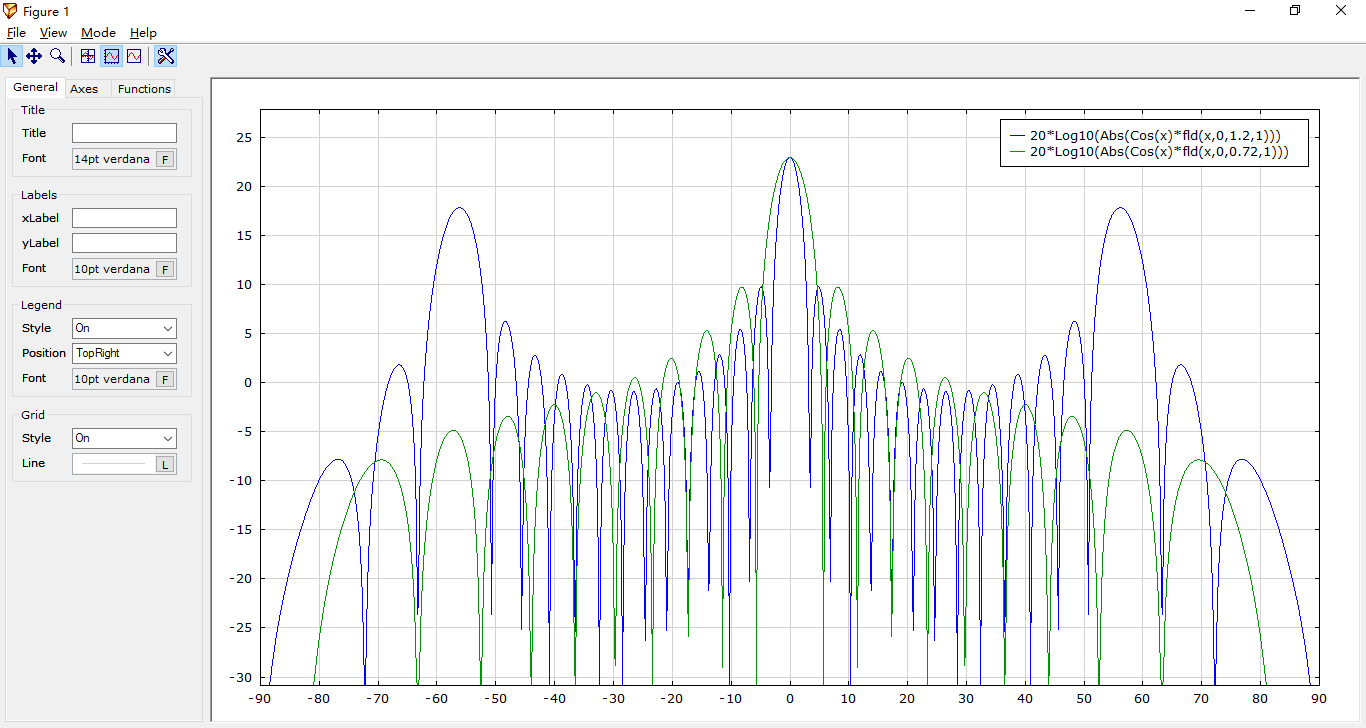
Then I plot array factor for two different element spacing's: DX=1.2 of wavelength and DX=0.72 of wavelength:
Plot(20*Log10(Abs(Cos(x)*fld(x,0,1.2,1))),xMin=-90,xMax=90) Plot(20*Log10(Abs(Cos(x)*fld(x,0,0.72,1))),xMin=-90,xMax=90)
As you can see, for DX=1.2 wavelength spacing there are huge grating lobes appear (blue plot). For DX=0.72 grating lobes are fully disappeared (green plot), but main lobe became wider:
One way to eliminate unwanted lobes is to use radiating elements which have low radiation pattern in side lobe direction. There are even cases when main lobe must be eliminated to form double-beam antenna using grating lobes. There are good articles on this topic:
1) DUAL-BEAM ARRAY ANTENNA BASED ON CIRCULAR PATCH ELEMENTS WITH CONICAL BEAM PATTERN
http://www.jpier.org/PIERM/pier.php?paper=14032601
2) Synthesis of unequally spaced printed antenna arrays by modeling of the feed network
https://www.researchgate.net/publica...e_feed_network
And some other useful links:
https://en.wikipedia.org/wiki/Passiv..._scanned_array
Very good online articles on this topic:
http://www.antenna-theory.com/arrays/main.php
http://www.antenna-theory.com/arrays/arrayfactor.php
