求帮忙推导二阶ΣΔADC的时域函数
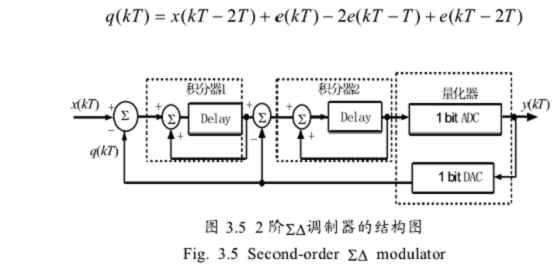 利用延时死活推不出来,有中间变量消不掉啊,请问底下的反馈是输出吗?有延时吗?是我哪个知识点不知道吗?求大神指点!挺急的,求指导!
利用延时死活推不出来,有中间变量消不掉啊,请问底下的反馈是输出吗?有延时吗?是我哪个知识点不知道吗?求大神指点!挺急的,求指导!
我没有推过。但是看你写出来的方程感觉上就是呀
Y=q=x*Z^-2 + e-2e*Z^-1+eZ^-2=x*Z^-2 + e(1-z^-1)^2
难道这个不是它的传递函数么?
楼上正解。用延迟方程转变成Z域的。
2L正解
额。可能我说错了,我的意思是上面那个延时方程是怎么搞出来的,而不是由延时方程推出Z域方程。
不是啊,是从框图如何推出上面的延时方程,而不是由延时方程到传递函数,那个由延时到Z变换我懂,哎,你们都不懂我!
亲,帮我推一下上面的延时方程,不是Z域传递函数!
針對每一個 x(n-m) Z轉換 X*z^-m 這是最基本的DSP 不會弄建議不要碰sigma delta
我是说时域的那个方程啊,不是z变换啊,那个我知道啊,你帮我推一下那个时域方程啊,我知道z变换啊
我推一下 好像弄錯了 等一下
z-transform of your figure in linear model.Y=STF*X+NTF*E
NTF=(1-z^-1)^2/(1-z^-1-z^-2)STF=z^-2/(1-z^-1-z^-2)
y(n)-y(n-1)-y(n-2)=e(n)-e(n-1)+x(n-2)我念書時常發現書上是錯的 paper 更多是錯的
这和给的z传递函数不一样哦,问题究竟在哪里?
我念書時常發現書上是錯的 paper 更多是錯的 這個paper就是一個大錯誤所以我常建議青年學子千萬不要相信paper的鬼扯
這完全證明我給各位青年學子的建議是正確無誤的
我就说呢。难道我看的文献都是错的,太可怕了吧
所以我常建議青年學子千萬不要相信paper的鬼扯
這完全證明我給各位青年學子的建議是正確無誤的盡信書不如無書 正如同我的簽名檔所言
Thinking is more important than reading.
哎,这个破问题纠结了我好久,没想到我看到paper都是错的。哎,太扯了。
正如同古人所言 上一次當學一次乖 paper大都是鬼扯的 那些亂寫paper的人為了拿學術點數 害人不淺
"paper大都是鬼扯的" 現在得到了千真萬確的証實
您有相當不錯的求知精神 值得嘉獎
可是我还要写paper
