关于近端串扰饱和长度的问题

最近在看Signal Integrity：Simplified的英文第2版，在近端串扰的饱和长度，英文版的的公式是len=1/2×RT×v，
v是动态线上信号传播速度，但在李玉山老师翻译的中文版上len=RT×v，不知道到底哪个是对的

len=1/2×RT×v 是对的

当然是len=1/2×RT×v，李玉山老师翻译的是英文第1版，Eric的英文第二版已经修正了这个错误，李玉山老师翻译的中文版第二版应该也快上市了，本来说2012年底上市，不知什么原因推迟了……
而且第一版仅近端串扰这一节就不止这一个错误，还有一个近端串扰持续的总时间也是有问题的（应该是2*TD+Tr），而且Eric的英文第二版也有没修正这个问题，我去！
这些大牛也是一样粗心，哈哈   

len=1/2×RT×v,是对的，从1/2×RT×v向后的回流回到近端的时间大于半个上升沿， be the signel，我就回不去参加叠加（近端的dV/dT还不等于0），所以到1/2处就到最大了，也就是饱和。

了解下！

您的意思我没搞太清楚，呵呵
1. 近端串扰的发生和上升/下降沿有绝对的关系，在电流不变的时候也就谈不上串扰
2. 近端串扰如果想叠加就需要前面的上升/下降沿产生的串扰已经返回来，而此时此位置的上升沿还没有完成，这样新产生的近端串扰就会叠加到返回的近端串扰上
3. 传输线末端的位置只能叠加刚刚返回的一点点近端串扰，离远端较远的地方会就叠加的多一点
4. 但是远到离远端距离1/2*Tr*v的位置时，上升/下降沿刚好在此处结束，此为近端串扰的最后一次叠加，近端串扰再往回传就到达信号电流维持不变的位置
5. 此时不会再产生新的串扰，近端串扰也就无法再叠加了，即此位置近端串扰达到最大值！

我又研究了下，确实应该是LEN=1/2×RT×v
关于近端串扰总时间的问题，我2个版本都看了下，我觉得没错啊，注意看配图，2TD并不包括下降沿

"远到离远端距离1/2*Tr*v的位置时，上升/下降沿刚好在此处结束，"  此时上升沿还未结束啊，还有一半时间吧。只是上升沿前端走到（1/2*Tr*v+Δlength）的回流回到近端需要的时间>1/2*Tr，就不能参与叠加。

哈哈 2*TD后面那个不是下降沿，也是上升沿产生的串扰，只是串扰越来越小了，其实图本身没有错，错的是第3条的说明，图上近端串扰持续总时间明显是2*TD+Tr，而第3条说明却说是2*TD
其实对TD>>Tr的情况，如TD=100*Tr，则持续总时间在这两种情况下相差不大，相对而言，Tr太小，可以忽略
但对于近端串扰刚好能达到最大值的情况即TD=0.5*Tr而言就不一样了，真正的近端串扰持续总时间明显是2*TD+Tr=2*0.5*Tr+Tr=2*Tr，而按第3条说明则是2*TD=Tr，足足差了一倍！

离远端距离1/2*Tr*v的位置时，上升/下降沿当然在此处就结束了，上升沿时间为Tr，从末端返回来到离远端距离1/2*Tr*v的位置需要0.5*Tr，而剩下的一半上升沿正停留在驱动线末端到离末端距离1/2*Tr*v的位置，所以离远端距离1/2*Tr*v的位置恰好为上升/下降沿结束的位置

呵呵 刚又仔细看了看，我说的在“此处”结束，不是“此时”，“此处”是驱动线离远端距离1/2*Tr*v的位置，此时上升沿还有0.5*Tr时间才能到达末端是毫无疑问，只是剩下的上升沿再产生的串扰叠加再也达不到最大值了，只会越来越小，最后上升沿到达末端时产生的近端串扰刚刚比0大一点，这最后一点近端串扰传回末端还需要TD的时间

另外，补充一点，近端串扰最大值产生的位置并不在传输线末端，而是在离末端0.5*Tr的位置，这也正是饱和长度的最短位置！

近端串扰分析的就是近端什么时候串扰达到最大，上升沿打入传输线，有电压/电流变化的地方就会有串扰。当两个传输线平行达到1/2*Tr*v时，串扰就会达到最大，原因见我上面的回复。Nelson的回复中提到"离远端距离"我就不明白了，后面怎么样暂时是不考虑的

近端串扰 对信号有什么影响  如何减少呢

谢谢，两位的讨论让我获益良多，PS，书上果然写错了，确实应该是2TD+Tr

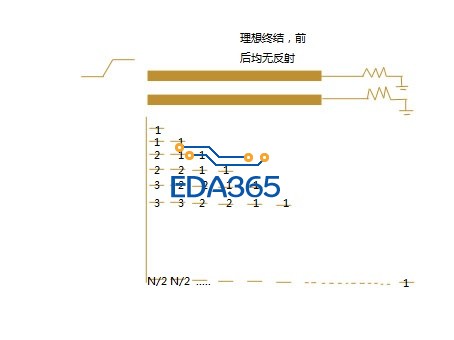
可以把驱动端的信号上升沿或下降沿平均分成N分，我们放慢动作让它一次只传Tr/N，从信号被打在传输线上开始把传输线也分为延迟Tr/N的相等的小段，那么信号在相邻传输线上产生的串扰可以分次分段计算，如下图所示，这里N为偶数，图中数字为串扰叠加次数，当信号完全进入传输线，这时信号达到饱和值，持续时间为Tr