关于信号反射的疑惑，求指点

假设入射电压为Vin，反射电压为Vre，传输电压为Vtr，入射电流为Iin，反射电流为Ire，传输电流为Itr。在阻抗不连续点的左右两侧的电压和电流相等，那么有 Vin+Vre=Vtr ①  Iin-Ire=Itr ②，这是有关信号反射一些资料上的解释。反射电流跟入射电流方向相反，②式中的负号我理解，既然反射电流跟入射电流方向相反，但①式中反射电压Vre为什么不是负的呢?

因为电压的正负只跟它的反射系数有关，跟能量的流向无关，电流的正负跟它的流向有关

其实不难理解。
Iin-Ire=Itr所以可以得到
(Vin/Z1)-(Vre/Z1)=Vtr/Z2
tao=(Z2-Z1)/(Z2+Z1)=Vre/Vin
推导一下不难推得
Vtr=Vin+Vre
Z1为端口前的阻抗，Z2为端口之后的阻抗
原本完整的
Vin=amplitude(Vin)*e^(-gamma*L)  
Vre=Vin*tao*e^(2*gamma*L)=amplitude(Vin)*e^(gamme*L)
gamma为传输常数，L为传输线相移长度
不管Vtr还是Itr在开始算复数形式时都满足
Vtr=Vi+Vr
Itr=Ii+Ir
只不过通常我们时域所关心的V和I为一个实数形式的矩量值，或者说电压大小，电流大小，而完整的时域形式是一个对数或者三角函数形式，来表征相移，幅度。在几组公式做微积分后自然就会使得矩量的反射电流上多出了一个负号。

首先，由
Iin-Ire=Itr所以可以得到.
(Vin/Z1)-(Vre/Z1)=Vtr/Z2①
tao=(Z2-Z1)/(Z2+Z1)=Vre/Vin②
推导出
Vtr=Vin+Vre③。
这个推导过程是不正确的，因为上述①③是推导反射系数用的。你再拿来反过去推导出③式，肯定得出Vtr=Vin+Vre的结论。
另外我查阅了于博士的《信号完整性揭秘》一书，讲到波传播的LC参数表示内容时，说根据傅里叶分解，数字信号的电压和电流可以分解为很多谐波分量，由此引出了信号电压的电报方程，电流也有类似的电报方程式。讲到这里我似乎明白了为什么电压是Vtr=Vin+Vre，而反射电流又表述为Iin-Ire=Itr，这与前面的电报方程又有矛盾，怎么解释?

这三组公式原本就是相关的，但是ERIC的书是偏工程应用，他不会说明的非常清楚每个公式的由来。
给你推导是方便你理解，而且反射系数这个定义是固定了Vre/Vin=(Z2-Z1)/(Z2+Z1),用来反推电流怎么算错?
至于你说的电报方程...是RLGC电导方程,
dv/dz
第二种方法我有提到。推导方法是RLGC微分电路模型加上瞬态电压电流定义。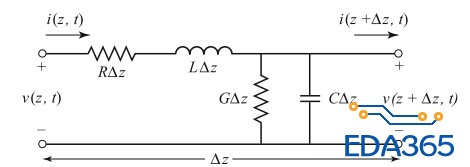

由基尔霍夫很容易得到
dV ( z )/dz= −( R + j ω L ) I ( z ),
然后由完整形式Vi，Vr，Ii，Ir的定义：
Vi=amplitude(Vin)*e^(-gamma*L)  
Vr=Vin*tao*e^(2*gamma*L)=amplitude(Vin)*e^(gamme*L)
Ii=amplitude(Iin)*e^(-gamma*L)  
Ir=Ii*tao*e^(2*gamma*L)=amplitude(Vin)*e^(gamme*L)
gamma为传输常数，L为传输线相移长度
不管Vtr还是Itr在开始算复数形式时都满足
Vtr=Vi+Vr=V(z)
Itr=Ii+Ir=I(z)
至于你说的矛盾，我说的很清楚，
“只不过通常我们时域所关心的V和I为一个实数形式的矩量值，或者说电压大小，电流大小，而完整的时域形式是一个对数或者三角函数形式，来表征相移，幅度。在几组公式做微积分后自然就会使得矩量的反射电流上多出了一个负号。”
Ire的定义是Vre/Z1,而最后推导的格式为Itr=Vi*e^(-gamme*L)/z1 - Vr*e^(-gamme*L)/z1
所以这个地方Ire=Vre/z1 = -Ir
这里Ire就是我们常说的电路中的反射电流为实数模，而Ir是最开始定义的复数形式或者波反射电流。

也就是说Itr=Vi*e^(-gamme*L)/z1 - Vr*e^(-gamme*L)/z1这个公式推导出来就是Itr=Iin-Ire对吧?