无线电数字信号处理与软件无线电技术综述

随着无线电数字信号处理技术的发展，以及新标准和协议不断公布，无线电通信在迅猛发展的同时，带来了新的挑战和机遇。在数字技术得到快速发展的同时，软件无线电关键技术以及无线电信号处理相关技术，也受到广泛关注。与此同时，无线电通信技术从WLAN以及UWB逐渐发展到WiMAX，以及从2G到3G，再到最近讨论的4G通信技术，这些都体现了无线电技术的发展，以及在实际中的应用，更体现出无线电技术的重要性。随着与网络技术融合的加快，使得无线电信号处理与软件无线电关键技术变得更加重要。

1 多速率数字信号的处理

宽带数字中频软件无线电的原理，是对宽带频谱范围进行数字化，但前提条件，是将带通采样定理与前置滤波器进行有机结合，达到设计效果。带通采样定理的应用降低了中频采样频率，同时满足需要，但如果采样频率寄生进行处理，就会对增加采样量化的降噪比，有助于设计目标的实现。所以要在两者之间寻找合理的平衡点，就需要把采样频率调高，同时使得瞬间采样带宽达到一定的带宽值。对于多速率信号的处理，基本理念中抽去以及内插理论技术变得十分重要。

1．1 有关数字信号速率的整数倍抽取

整数倍抽取的定义，就是把原始采样序列x(n)每隔D-l个数据取一个，从而形成一个全新的序列x，也就是

xD(m)=x(mD) (1)

式中，D为正整数。若x(n)序列的采样率取sf，则其无模糊带宽则为fs／2。根据计算公式，可以得出，抽取序列的频谱XD(ejω)，是由抽取之前原始序列频谱X(ejω)，经过频率转移并且进行D倍展宽，最后由D个频谱叠加得到。

经上述的分析，可得到如图1所示，带宽<πD的低通滤波器。如果原始信号的频谱分量<π(I)，就可以将前置低通滤波器省略。

1．2 数字信号处理的整数倍内插

对于数字信号处理的整数倍内插，就是在两个原始抽样点之间插入(I-1)个零点，这就是整数倍内插如果原始抽样序列是x(n)，那么经过整数倍内插后的序列可通过相应的数学表达式进行表达，但是可以画出内插、经过压缩后的频谱如图3所示。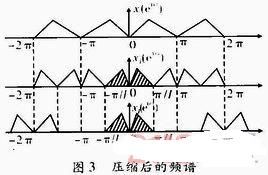

1．3 关于采样率的分数倍变换

上述数字处理技术，均为抽去和内插之间的特殊关系，实际是采样率变换方式中的一种特殊变换：整数倍变换，实际还存在着分数倍变换。如果分数倍变换比R=RD／I。那么可以进行完I倍内插后，再进行D倍抽取得到设计效果，但须注意内插与抽取的顺序需要特别规定，即先进性内插，再进行抽取。就可以保证，中间序列的基带频谱宽度大于原始信号频谱的基带谱宽度，达到设计要求，否则会导致信号失真。

1．4 关于抽样率转换的多级实现

经过多级变换实现高倍数抽取系统，可分为两个途径，第一种是寻求最优化的方法，根据每秒钟的乘法次数作为基准，找出各级内部最佳的抽取以及内插因子，完成对各级滤波器的设计。第二种是通过抽取或者内插器进行处理，这种抽取器的抽取因子为2。同时这种抽取以及内插因子为2的抽取以及内插器，可使用半带滤波器进行有效的滤波，并且，对于这种带有冲击响应的滤波器，其中有近1／2冲击响应的值为0对于抽样率转换系统而言，它的总抽取因子，并不是在任何情况下，都可以用2的幂次方进行表示，但用某个整数与2的幂次方的乘积进行表示确是可行的，因此在能够多绒实现抽样率转换系统中，就会出现抽取或内插因子是一个整数的抽取或者内插器。在这类的抽取以及内插器中，一股都是通过积分梳状滤波器实现抗混叠以及去镜像滤波的。

1．5 正交变换的有关理论

对于在自然界中可实现的信号都称为实信号，实信号的频谱具有共轭对称性，是指实信号的征服频率是堆成的，分量正好相反。依据此特性，对于任何实信号，都可对某一部分作相应的描述，然而不会丢失任何信息，也不会产生虚假信号。

数字上下变频器采用的基本处理方法，就是对信号进行分解、信号分析以及调制解调。但实际中较难找到理想的，通过Hilbert变换的阶跃滤波器，以至于数字信号处理经常采用正交分解进行处理，就是数字序列(fn)和两个正交本振序列cos(o)t和sin(o)t经过相乘后，凭借着数字低通滤波来实现。由于结果是两个正交本振序列和的乘积，所以就保证其正交性。此外，从工作原理上，数字上下变频慨念，就是把输入的数字信号以及一个本地震荡数字信号，经过相乘完成频谱转移。这种技术内容主要包括：数字控制振荡器、数字混顿器以及低通滤波器。通信系统中无线电信号处理与软件无线电技术密不可分，只有掌握才能更好地在科技生产中适应潮流发展。然而对于软件无线电技术，应尽量将其放在一个开放软件平台上，实现其功能。在尽可能靠天线近的地方