矩形波导宽边四元斜缝天线的设计

引言

　　波导缝隙天线具有口面场分布容易控制，没有能量漏失、天线口径效率高、性能稳定、结构简单紧凑、强度高、安装方便、抗风力强等优点，而且容易实现窄波束、赋形波束、低副瓣乃至超低副瓣，所以波导缝隙天线已经成为新型雷达中天线的优选形式，被广泛应用于雷达和通讯领域。该天线要求在水平面内具有宽波束的特点，能够覆盖比较宽的范围，从而更有效地提高车辆的战场生存能力。天线需要满足的性能指标如下：a.增益：大于11dB；b.3dB波束宽度：E面为20°，H面为110°；c.副瓣电平：小于-13dB；d.驻波比：小于2。

　　波导缝隙天线是一种重要的微波天线，在通信和雷达系统中获得了广泛的应用。然而，随着波导缝隙数目的增加，单纯依靠仿真软件或是数值方法，在普通PC机上都很难进行分析。因此，对大型波导缝隙天线快速高效的分析计算成为工程上的迫切需要。本文基于广义导纳矩阵（GAM），围绕大型波导缝隙天线的快速分析展开了研究：本文首先采用模式匹配的经典理论，建立了以波导缝隙天线裂缝所在平面法线方向为参考方向的分析模型，将天线分成内外两个区域。对于天线内部区域，提出了行波状态利谐振状态两种情况下波导缝隙天线内部区域广义导纳参数的快速提取方案，建立了具有广泛适用性的天线单元广义导纳参数数据库，实现了缝隙天线内部区域GAM的级联，得到了广义输入导纳等主要参数，与HFSS仿真结果吻合良好。

　　1 理论分析

　　1.1 串联缝隙阵的模型

　　由波导内的场分布情况可知：当波导宽边中心开斜缝时，窄缝在纵向不切割电流线；在缝的横向由于对电场的扰动，使得总电场在缝的两侧发生跳变，即电压跳变，故相当于在传输线上串联了一个阻抗。对中心馈电的谐振线阵模型来说，假设波导壁上开有Ⅳ爪斜缝，缝与缝中心间距λg／2，为取得同相激励，相邻缝交叉倾斜放置，波导末端短路板距终端缝隙λg／2，以使缝隙中心处于电压或电流最大值位置，线阵模型如图1所示。

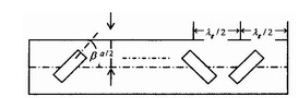
图1:线阵模型

其等效电路如图2所示。

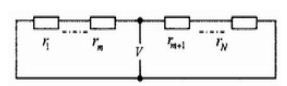
图2:等效电路

图中所示均为归一化的等效电阻。

　　1.2 缝隙特性参数的分析

　　在天线工作频率的选取上，本雷达系统的工作频率为10.5GHz，故该天线的工作频率为10.5GHz，，对于阵列中各单元以等间距位于直线上的线阵，其阵列因子可表示为：

阵列因子

其中An为激励的幅度，θ为观察方向与直线的夹角，d为阵元间距。由于谐振阵各单元是同相的，即φn=O，则上式可简化为：

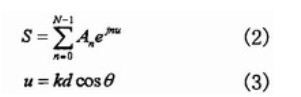
阵列因子

当u=2mπ，m=O，±1，…时，S取最大值，且m=0时为主瓣。为了实现低副瓣并使主瓣展宽，采用中心馈电从阵中到边缘幅度递减，按泰勒线源分布加权各缝隙，两边呈对称分布，其方向图零点位置由下式决定：

方向图零点位置计算式

将后一项按多项式展开，Z的各次幂系数即为相对应的激励幅度。

　　由图2，当波导采用中心馈电并处于谐振的时候（其阻抗虚部为零），对泰勒分布而言，则有：

泰勒分布计算式

将之前得到的每个缝隙的激励幅度代入即可求得相应的归一化电阻值，在本设计中N取4。

　　A.F.STevensON利用洛伦兹互易定理及波导中功率的平衡方程，得到了串联缝隙的归一化等效电阻表示式为：

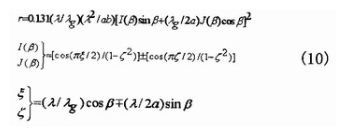
归一化等效电阻表示式

其中β表示缝隙中心线与波导宽边中心线之间的夹角，α为宽壁的长度，b为窄壁的长度。将之前求得的rn代入并求解方程可得到对应的缝隙偏角。

　　1.3 影响天线性能的因素

　　应用以上所计算出来的结果来进行天线的设计，还必须考虑缝隙间的互耦问题；若不考虑互耦，将使天线口径面的幅度分布和相位分布变坏，同时也将恶化天线的输入端匹配。

　　串联缝隙与纵向缝隙相比，由于其角度偏转的原因，其交叉极化辐射要比纵向缝隙高，这会带来副瓣电平的升高和增益的降低，仿真结果也证实了这一点，而这是我们在设计中所不希望看到的，需要采取措施抑制交叉极化辐射。在本设计中，采用在每个缝隙上方加一个小波导口的办法，小波导的传播方向垂直于缝隙所在的平面。

2 建模与仿真

　　本文在设计波导缝隙天线的过程中，设计中的数值仿真都是在CST时域求解器的环境中完成的。

　　2.1 天线模型的建立

　　辐射波导选用的尺寸是22.86×10.16mm，缝一侧的波导壁厚1mm，缝宽为2mm，波导两端为理想短路面；截止波导16×8mm。建立模型，其框架图如图3所示：

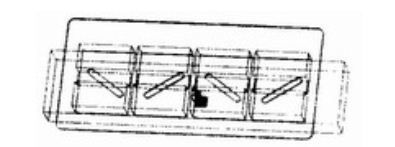
天线模型框架图

其中黑色标记处为同轴线中心馈电点；辐射口上方的方形材料为天线罩；从左到右缝隙的编号依次为1～4。

　　2.2 仿真结果分析

仿真中将缝长l和倾角β设置成变量，l的初始值取λ／2，利用CST的参数扫描功能，对缝隙长