基于信息熵的Markov网络结构学习算法研究
时间:11-25
来源:电子设计工程
点击:
4 基于信息熵的Markov网构造算法
给定一样本集(n个属性的一张二维表),先对系统中N个变量构建一个完全无向图氏,然后利用信息独立测试理论有效删剪PG图,以得到所求的Markov网。
首先给出这个算法所需要的一些假设:给定的样本数据集D是完整的;所有的变量取值均为离散性,若取值连续可先进行离散化。
第1步:构造完全有向图
定义8:设一个系统含有N个变量{X1,X2,……,Xn},完全有向图PG={<Xi,Xj>|,其中i,j=1,2,…,n且i≠j,<Xi,Xj>表示Xi与Xj有因果关系Xi→Xj}。由此定义可知,PG是一个I-图。
第2步:有效删剪PG图
从定理3的性质2可得到一个判断X,Y是否条件独立的算法:当给出一个概率分布P(x)时,可通过判断I(X,Y|Z)=0代替I(X,Y|Z),从而PG图中的X→Y和Y→X边可删除;否则。在给定条件Z的情况下,X和Y互相依赖。然而在实际计算中并没有一个真正的概率分布P(x),只有一个基于样本数据集D而计算的一个经验概率分布PD(x)近似估计P(x),计算的I(X,Y|Z)只是基于PD(x)上的I(X,Y|Z)近似值,所以其值总大于0。为此,判断条件独立方法可描述为:
定理4:设X,Y,Z为全集U上3个不相交的子集,基于样本数据集D上概率分布PD(x),如果有:I(X,Y|Z)<ε,则判定给定Z,X与Y条件独立;否则给定Z,X与Y是条件依赖的。其中ε为一个阈值,通常取一个很小的正数。
由定理4可知,经这一步删减,在不考虑边的方向情况下,PG图是一个最小I-图,即所要构造的Markov网。其算法如下:
(1)输入样本数据集D,节点集U,阈值ε1
(4)输出V
由以上算法可知:整个算法是计算复杂度为O(/N2)的条件独立性CI(Conditional Independence)测试。
5 实例分析
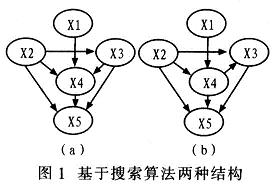
此例来自对华盛顿高级中学131名高年级学生的升学计划调查,每个学生用下列变量及其相应的状态来描述:性别(X1):男、女;社会经济状态(X2):低、中下、中上、高:智商(X3):低、中下、中上、高;家长的鼓励(X4):低、高;升学计划(X5):是、否。样本数据:下面的数据表示对5个变量取值的某种组合统计所得到的人数,例如:第一个数据4表示对(X1=男,X2=低,X3=低,X4=低,X5=是)这种组合所统计出的人数。变量依次按从右到左的顺序轮换,状态则按照上述所列各变量状态的顺序进行轮换,依此类推,得到完全统计数据如下:4,349,13,64,9,207,33,72,12,126,38,54,10,67,49,43,2,232,27,84,7,201,64,95,12,115,93,92,17,79,119,59,8,166,47,91,6,120,74,110,17,92,148,100,6,42,198,73,4,48,39,57,5,47,123,90,9,41,224,65,8,17,414,54,5,454,9,44,5,312,14,47,8,216,56,35,13,96,28,24,11,285,29,61,19,236,47,88,12,164,62,85,15,113,72,50,7,163,36,72,13,193,75,90,12,174,91,100,20,8l,142,77,6,50,36,58,5,70,110,76,12,48,230,81,13,49,360,98Heckerman等用基于统计打分搜索算法得到如图1所示的两种最有可能的结构。
基于图1所示的算法计算结果如下:取阈值为0.007和0.001,经计算得到图2a的结构,根据专家知识可知:性别、社会经济状态是不会有父节点的,所以对X1<=>X4和X2<=>X3两种依赖关系可修订为X1=>X4和X2=>X3,由此得到图2b所示的结构。因此,可以看出,图1a和图2b是一样的。根据Markov的理论和特征,得到Markov网结构,如图3所示。
6 结束语
通过认真研究信息熵理论知识得到基于信息熵的Markov网算法,在一定程度上简化了Bayesian网推理过程,提高了推理效率,对知识的不确定推理研究具有参考价值。
编辑:小宇
给定一样本集(n个属性的一张二维表),先对系统中N个变量构建一个完全无向图氏,然后利用信息独立测试理论有效删剪PG图,以得到所求的Markov网。
首先给出这个算法所需要的一些假设:给定的样本数据集D是完整的;所有的变量取值均为离散性,若取值连续可先进行离散化。
第1步:构造完全有向图
定义8:设一个系统含有N个变量{X1,X2,……,Xn},完全有向图PG={<Xi,Xj>|,其中i,j=1,2,…,n且i≠j,<Xi,Xj>表示Xi与Xj有因果关系Xi→Xj}。由此定义可知,PG是一个I-图。
第2步:有效删剪PG图
从定理3的性质2可得到一个判断X,Y是否条件独立的算法:当给出一个概率分布P(x)时,可通过判断I(X,Y|Z)=0代替I(X,Y|Z),从而PG图中的X→Y和Y→X边可删除;否则。在给定条件Z的情况下,X和Y互相依赖。然而在实际计算中并没有一个真正的概率分布P(x),只有一个基于样本数据集D而计算的一个经验概率分布PD(x)近似估计P(x),计算的I(X,Y|Z)只是基于PD(x)上的I(X,Y|Z)近似值,所以其值总大于0。为此,判断条件独立方法可描述为:
定理4:设X,Y,Z为全集U上3个不相交的子集,基于样本数据集D上概率分布PD(x),如果有:I(X,Y|Z)<ε,则判定给定Z,X与Y条件独立;否则给定Z,X与Y是条件依赖的。其中ε为一个阈值,通常取一个很小的正数。
由定理4可知,经这一步删减,在不考虑边的方向情况下,PG图是一个最小I-图,即所要构造的Markov网。其算法如下:
(1)输入样本数据集D,节点集U,阈值ε1

(4)输出V
由以上算法可知:整个算法是计算复杂度为O(/N2)的条件独立性CI(Conditional Independence)测试。
5 实例分析
此例来自对华盛顿高级中学131名高年级学生的升学计划调查,每个学生用下列变量及其相应的状态来描述:性别(X1):男、女;社会经济状态(X2):低、中下、中上、高:智商(X3):低、中下、中上、高;家长的鼓励(X4):低、高;升学计划(X5):是、否。样本数据:下面的数据表示对5个变量取值的某种组合统计所得到的人数,例如:第一个数据4表示对(X1=男,X2=低,X3=低,X4=低,X5=是)这种组合所统计出的人数。变量依次按从右到左的顺序轮换,状态则按照上述所列各变量状态的顺序进行轮换,依此类推,得到完全统计数据如下:4,349,13,64,9,207,33,72,12,126,38,54,10,67,49,43,2,232,27,84,7,201,64,95,12,115,93,92,17,79,119,59,8,166,47,91,6,120,74,110,17,92,148,100,6,42,198,73,4,48,39,57,5,47,123,90,9,41,224,65,8,17,414,54,5,454,9,44,5,312,14,47,8,216,56,35,13,96,28,24,11,285,29,61,19,236,47,88,12,164,62,85,15,113,72,50,7,163,36,72,13,193,75,90,12,174,91,100,20,8l,142,77,6,50,36,58,5,70,110,76,12,48,230,81,13,49,360,98Heckerman等用基于统计打分搜索算法得到如图1所示的两种最有可能的结构。
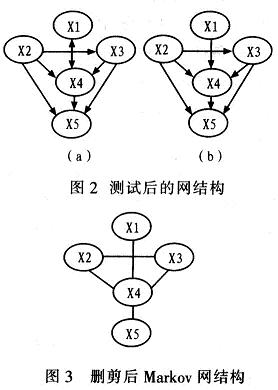
基于图1所示的算法计算结果如下:取阈值为0.007和0.001,经计算得到图2a的结构,根据专家知识可知:性别、社会经济状态是不会有父节点的,所以对X1<=>X4和X2<=>X3两种依赖关系可修订为X1=>X4和X2=>X3,由此得到图2b所示的结构。因此,可以看出,图1a和图2b是一样的。根据Markov的理论和特征,得到Markov网结构,如图3所示。
6 结束语
通过认真研究信息熵理论知识得到基于信息熵的Markov网算法,在一定程度上简化了Bayesian网推理过程,提高了推理效率,对知识的不确定推理研究具有参考价值。
编辑:小宇
