基于DSTFT的FSK信号的解调
时间:05-08
来源:现代电子技术
点击:
1 引言
移频键控(FSK)是数字通信中一种常见的调制方式,由于它解调延时短、电路设计简单、易于实现而且具有较强的抗干扰和抗衰落的能力,因而广泛地应用于电力线载波通信及公用交换网上的数据通信等中低速远程数据通信中。在传统的移频键控信号的数字解调理论中,可以分为两大类:一类是相干方式解调,另一类是非相干方式解调。相干数字解调接收质量最佳,但在其解调过程中恢复出具有精确频率和相位的相干信号较为困难,所需设备也较复杂。而采用非相干数字解调方法,可根据数字移频键控信号的特点,在接收端不需要相干信号,因而被广泛使用。但是现有的解调2FSK信号的方法,大多采用时域解调的方式,本文提出了一种利用离散短时傅里叶变换(DSTFT)在时域和频域解调2FSK信号的新方法。
2 利用DSTFT方法解调2FSK信号
2.1 离散短时傅里叶变换
离散短时傅里叶变换定义为:
其中:x(n)为输入信号序列,w(n)为移动窗函数,N为窗宽度。由式(1)可见,DSTFT实际上是加移动窗的离散傅里叶(DFT)变换,窗函数w(n)一般对窗中心对称,其作用是取出x(n)在n时刻附近的一小段信号进行傅里叶变换。
短时傅里叶变换具有明显的物理意义,它可以看作是信号x(n)在"分析时间"n附近的"局部频谱",当n变化时,得到信号频率随时间n变化的规律。可以看出,DSTFT将时域和频域组合在一起,反映了某一时间点附近的频率分布情况,因而可以提取频率局域化信息。
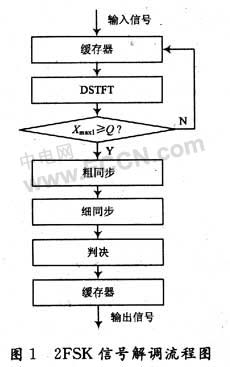
根据DSTFT的原理,提出了一种用它解调BFSK信号的方案,整个系统实现框图如图1所示。
2.2 判决算法
典型的2FSK离散数字信号可表示为:
其中,A(i)代表第i个码元,N代表码元宽度,f1和f2是信号的两个载频(分别代表数据0,1),fs是采样率。
信号的2个载波频率点分别为K1=[Nf1/fs]和K2=[Nf2/fs]([?]表示取整)。频率点的幅度值为:
如果∣X(nN,K2)∣>∣X(nN,K1)∣,判为码元1,否则判为0,这样解调虽然简单,但需要精确的码元同步(即采样起始点在两个码元连接点上)。信号采样起始点具有很大的随机性,并不能保证从码元起始变化点开始采样。所以码元同步是解调的关键所在。
对于利用DSTFT实现2FSK信号解调,码元同步是其中的关键。文献[3]中的同步算法,利用信号载频处的频谱峰值比计算出同步指针的大小,得到定时偏差实现码元同步。这种方法原理简单,运算量较小,在没有噪声和频谱泄漏的情况下,计算出的调整指针比较精确。但是在低信噪比的情况下,这样直接计算同步调整指针,误差会比较大,会影响后面的码元判决。因此这种方法只适用于信噪比比较高,同步不要求很精确的情况。
我们提出了一种新的同步算法,这种同步算法适用于码元速率比较低,码元宽度比较长的情况。同步过程分为粗同步和细同步,取窗口长度为码元宽度Ns。
粗同步时,窗口移动步长以Ns/8为例,每次移动后计算数字频率点Ki(i=1,2)的频谱峰值,因此对一个码元,最多移动8次,即可找到其最大值:
其中,X(m,Ki)表示分析窗移动m次时频率点Ki的频谱,然后记录下最大频谱峰值Xmax1,与设定的门限值Q进行比较,如果Xmax1<Q,则判断不是有效信号,继续搜索信号;如果Xmax1≥Q,则认为接收到了2FSK信号,这时记录下最大频谱峰值对应的分析窗移动次数m,就实现了粗同步。
细同步是在粗同步的基础上,改变窗口的移动步长为1,移动范围为窗口所在位置的前后Ns/16宽度,每次移动后同样计算数字频率点K(K是代表0或1的频率点在粗同步时已经确定了)的频谱峰值,最多移动Ns/8次,即可找到频率点K的最大频谱值(p代表窗口移动次数):
这时就实现了码元的细同步,也完成了整个的同步过程。
实现同步后,改变窗口的移动步长为Ns,每次移动后计算该码元在数字频率点0和1处的频谱值,然后进行判决,实现实时解调。
3 试验仿真
基于上述原理,使用Matlab R2006a进行仿真试验。假设2FSK信号的载波频率是精确的,参数如下:
f1=2 000 Hz,f2=4 000 Hz,采样频率fs=80 000 Hz,码元速率R=1 000 b/s,噪声为加性高斯白噪声。
图2为采用DSTFT、非相干解调和相干解调法解调上述的2FSK信号时不同信噪比对应的误码率关系。
从图2中可以看出,采用DSTFT解调的性能比一般的非相干解调好,而与相干解调法相比,在信噪比低于0 dB时,相干解调法性能较好,信噪比高于0 dB时,DSTFT解调性能较好。对比其他非相干解调法,DSTFT的性能优势明显,而且解调方法简单明了,而对比相干解调法,DSTFT在解调性能上有一点差距,但相干解调所需的设备复杂,实现精确解调付出的代价比DSTFT大。因而总体来讲,DSTFT是一种实用的BFSK解调法。
本文讨论DSTFT方法解调BFSK信号时,采用的窗函数是矩形窗,但运用DSTFT进行时频分析时,窗函数的时频特性将直接影响到信号的频谱,从而对解调性能产生影响,因而,笔者认为接下来的工作中,可以采用不同的窗函数进行解调,进一步优化DSTFT的解调算法,达到更佳的解调性能。
移频键控(FSK)是数字通信中一种常见的调制方式,由于它解调延时短、电路设计简单、易于实现而且具有较强的抗干扰和抗衰落的能力,因而广泛地应用于电力线载波通信及公用交换网上的数据通信等中低速远程数据通信中。在传统的移频键控信号的数字解调理论中,可以分为两大类:一类是相干方式解调,另一类是非相干方式解调。相干数字解调接收质量最佳,但在其解调过程中恢复出具有精确频率和相位的相干信号较为困难,所需设备也较复杂。而采用非相干数字解调方法,可根据数字移频键控信号的特点,在接收端不需要相干信号,因而被广泛使用。但是现有的解调2FSK信号的方法,大多采用时域解调的方式,本文提出了一种利用离散短时傅里叶变换(DSTFT)在时域和频域解调2FSK信号的新方法。
2 利用DSTFT方法解调2FSK信号
2.1 离散短时傅里叶变换
离散短时傅里叶变换定义为:
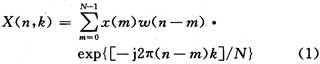
其中:x(n)为输入信号序列,w(n)为移动窗函数,N为窗宽度。由式(1)可见,DSTFT实际上是加移动窗的离散傅里叶(DFT)变换,窗函数w(n)一般对窗中心对称,其作用是取出x(n)在n时刻附近的一小段信号进行傅里叶变换。
短时傅里叶变换具有明显的物理意义,它可以看作是信号x(n)在"分析时间"n附近的"局部频谱",当n变化时,得到信号频率随时间n变化的规律。可以看出,DSTFT将时域和频域组合在一起,反映了某一时间点附近的频率分布情况,因而可以提取频率局域化信息。
根据DSTFT的原理,提出了一种用它解调BFSK信号的方案,整个系统实现框图如图1所示。
2.2 判决算法
典型的2FSK离散数字信号可表示为:
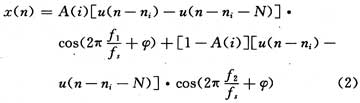
其中,A(i)代表第i个码元,N代表码元宽度,f1和f2是信号的两个载频(分别代表数据0,1),fs是采样率。
信号的2个载波频率点分别为K1=[Nf1/fs]和K2=[Nf2/fs]([?]表示取整)。频率点的幅度值为:
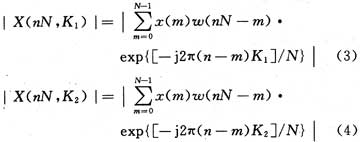
如果∣X(nN,K2)∣>∣X(nN,K1)∣,判为码元1,否则判为0,这样解调虽然简单,但需要精确的码元同步(即采样起始点在两个码元连接点上)。信号采样起始点具有很大的随机性,并不能保证从码元起始变化点开始采样。所以码元同步是解调的关键所在。
对于利用DSTFT实现2FSK信号解调,码元同步是其中的关键。文献[3]中的同步算法,利用信号载频处的频谱峰值比计算出同步指针的大小,得到定时偏差实现码元同步。这种方法原理简单,运算量较小,在没有噪声和频谱泄漏的情况下,计算出的调整指针比较精确。但是在低信噪比的情况下,这样直接计算同步调整指针,误差会比较大,会影响后面的码元判决。因此这种方法只适用于信噪比比较高,同步不要求很精确的情况。
我们提出了一种新的同步算法,这种同步算法适用于码元速率比较低,码元宽度比较长的情况。同步过程分为粗同步和细同步,取窗口长度为码元宽度Ns。
粗同步时,窗口移动步长以Ns/8为例,每次移动后计算数字频率点Ki(i=1,2)的频谱峰值,因此对一个码元,最多移动8次,即可找到其最大值:
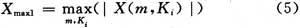
其中,X(m,Ki)表示分析窗移动m次时频率点Ki的频谱,然后记录下最大频谱峰值Xmax1,与设定的门限值Q进行比较,如果Xmax1<Q,则判断不是有效信号,继续搜索信号;如果Xmax1≥Q,则认为接收到了2FSK信号,这时记录下最大频谱峰值对应的分析窗移动次数m,就实现了粗同步。
细同步是在粗同步的基础上,改变窗口的移动步长为1,移动范围为窗口所在位置的前后Ns/16宽度,每次移动后同样计算数字频率点K(K是代表0或1的频率点在粗同步时已经确定了)的频谱峰值,最多移动Ns/8次,即可找到频率点K的最大频谱值(p代表窗口移动次数):
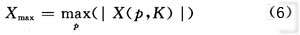
这时就实现了码元的细同步,也完成了整个的同步过程。
实现同步后,改变窗口的移动步长为Ns,每次移动后计算该码元在数字频率点0和1处的频谱值,然后进行判决,实现实时解调。
3 试验仿真
基于上述原理,使用Matlab R2006a进行仿真试验。假设2FSK信号的载波频率是精确的,参数如下:
f1=2 000 Hz,f2=4 000 Hz,采样频率fs=80 000 Hz,码元速率R=1 000 b/s,噪声为加性高斯白噪声。
图2为采用DSTFT、非相干解调和相干解调法解调上述的2FSK信号时不同信噪比对应的误码率关系。

从图2中可以看出,采用DSTFT解调的性能比一般的非相干解调好,而与相干解调法相比,在信噪比低于0 dB时,相干解调法性能较好,信噪比高于0 dB时,DSTFT解调性能较好。对比其他非相干解调法,DSTFT的性能优势明显,而且解调方法简单明了,而对比相干解调法,DSTFT在解调性能上有一点差距,但相干解调所需的设备复杂,实现精确解调付出的代价比DSTFT大。因而总体来讲,DSTFT是一种实用的BFSK解调法。
本文讨论DSTFT方法解调BFSK信号时,采用的窗函数是矩形窗,但运用DSTFT进行时频分析时,窗函数的时频特性将直接影响到信号的频谱,从而对解调性能产生影响,因而,笔者认为接下来的工作中,可以采用不同的窗函数进行解调,进一步优化DSTFT的解调算法,达到更佳的解调性能。
