基于DSP的混合型有源电力滤波器设计

  随着工业电力电子技术的发展，电力系统的谐波抑制和无功补偿问题越来越受到人们的广泛关注。传统的谐波抑制手段是在电网中加装无源电力滤波器PPF(Passive Power Filter),利用电感、电容的谐振特性，在阻抗分流回路中形成低阻抗支路，从而减小非线性负载向电网注入谐波电流。但无源滤波支路的存在只能对特定次谐波进行滤除、易与电网发生串联谐振等缺点，因而逐渐被有源电力滤波器APF(Active Power Filter)所取代[1]。有源电力滤波器虽能克服无源电力滤波器存在的缺陷，但其安装容量受开关器件容量的限制，当所需处理的谐波和无功电流较大时，由逆变器实现的技术难度和成本都将增加，从而限制了有源电力滤波器在大型供配电系统中的应用。

基于无源滤波器和有源滤波器的优点，将LC无源滤波器和有源滤波器结合起来形成一种混合型有源电力滤波器HAPF(Hybrid Active Power Filter),取两者之长、补其之短，把无功补偿和谐波抑制融为一体是一种完美的构想。但目前人们所提出的混合型有源电力滤波器的拓扑结构仍有不足之处。本文即针对目前常见的一种混合型有源电力滤波器结构进行了改进。

1 主电路结构和原理

1．1 主电路结构

目前常用的一种混合型滤波器的结构如图1所示，其工作原理可参考文献[2]。

该电路拓扑可通过控制晶闸管的开通和关闭来调整晶闸管投切滤波器TSF（thyristor switched filter）的结构，使得能量较大的低次谐波和无功功率主要由TSF补偿，APF主要作用是抑制剩余谐波，并改善TSF的滤波器特性。实际上，采用如图1所示的有源电力滤波器，将由于变压器的耦合作用，使所有的基波无功电流都流过有源电力滤波器。这样就迫使逆变器所需求的容量大大增加，必然增加逆变器实现的技术难度和成本，从而限制了有源电力滤波器在大型供配电系统中的应用。

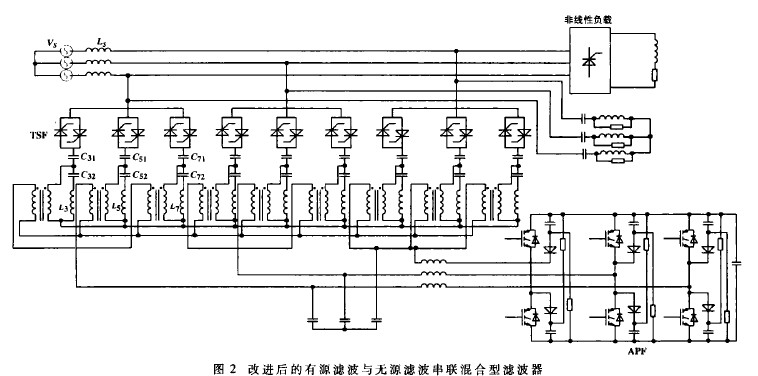
为了进一步降低有源电力滤波器的容量，可以在并联混合型有源电力滤波器的基础上结合它的注入电路方式将主电路的拓扑结构加以改进，改进后的系统结构如图2所示。它将逆变器的输出电压通过变压器耦合到无源滤波器的3次、5次、7次滤波支路的电感和电容两端。因为根据大量谐波源的频谱分析可知，谐波源能量主要集中在较低次谐波频率上，电力系统中谐波电流主要是由5次、7次的谐波滤波器来配置，其次是3次、11次、13次的谐波滤波器[3]，故本文TSF部分的电感和电容参数的选择按照无功功率补偿的需要，以3次、5次和7次谐波滤波器来配置，可以组成多级补偿状态，根据负荷无功电流的大小，由晶闸管投切来达到分级补偿的目的。这样，TSF在工频状态时为无功补偿状态，全谐振和脱谐时为滤波状态，既可以补偿又可以滤除谐波。 图2中，C31、C32和L3组成的LC滤波支路调谐在3次谐波频率，而L3和C32调谐在基波频率。这样，利用L3和C32对基波谐振的特性，使有源电力滤波器既不承受基波电压也不承受基波电流，从而极大地减小了有源电力滤波器的容量，降低了有源谐波补偿系统的投资，提高性能价格比，达到APF实用化的目的。5次和7次谐振支路的补偿原理与3次谐振支路相同。


1．2 滤波原理分析

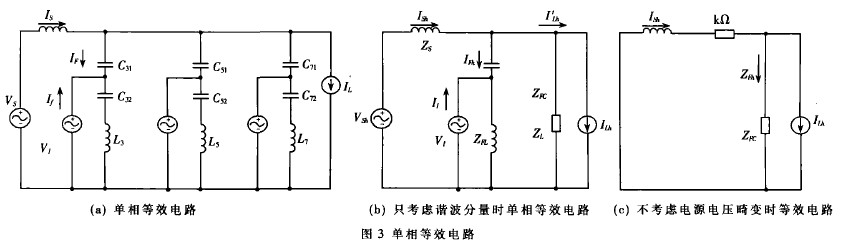
图2中的并联混合型有源电力滤波器的单相等效电路如图3(a)所示。这里假设有源电力滤波器是一个理想的受控电压源,谐波源被看作一个电流源IL。图中,C31、C32和L3分别为无源滤波器3次支路上的电容和电感。图3(b)为只考虑电网谐波电流分量时的单相等效电路图。ZS、ZFC、ZFL、ZL分别为电网阻抗、电容C31的阻抗、C32和L3的串联阻抗（呈感性）、5次和7次滤波支路总的等效阻抗（对高次谐波呈感性）。由图3(b)并根据基尔霍夫定律可写出如下方程：

从(6)式可以看出，当ILh、USh为定值时，如果K增大，ISh将减小。当K值足够大时，大部分负载谐波将流入无源滤波器，达到了很好的滤波效果。而且，当不考虑系统电压畸变引起的谐波电流时，即USh=0时，从式(7)可以看出，对于ISh而言，图3(a)和图3(c)是等效的。由图3(c)可以看出，这相当于在电网支路中串联了一个纯电阻K，因此，必然有更多的谐波电流流入无源滤波器。如果K>>|ZFC|，则由负载产生的谐波电流将流入LC滤波器；如果K>>|Z′S|，则滤波特性由K决定。此外，K还起到阻尼Z′S和ZF并联谐振的作用。


2 基于DSP的检测与控制系统

2.1 谐波及无功电流的检测

一般电网电流的组成可描述如下：

式中,ispf为瞬时基波有功电流；isqf为瞬时基波无功电流；ish为瞬时总谐波电流。除ispf外，isqf和ish应设法消除。如果能检测出is和ispf，则isqf与ish之和可以由isqf+ish=is-ispf算出[3]。