德州仪器电源设计中快速完成并-串联阻抗转换的方案

        本文将向您介绍如何快速地将并联阻抗转换为串联阻抗（反之亦然）。文章还说明作为频率函数的这一转换的图示看起来很像是史密斯圆（Smith Chart）。在简化变压器等效电路或滤波器网络到两个端器件过程中，本文介绍的方法较为有用。图1显示了将并联电路转换为串联电路的转换方程式（推导过程请参见附录1）。

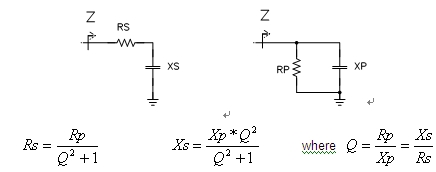
　　图1：这些电路为一个频率的等效电路。

       有趣的是，如果并联组件之一固定而另一个从开路到短路均不同，则这些表达式在Rs/Xs串联层中会形成一些圆。差异可以来自组件值的改变，也可以产生自随频率变化的组件阻抗。图2显示的是这些差异的举例。X轴代表串联电阻，而Y轴代表串联电抗。

        此处共有2个圆：一个代表恒定并联电阻，另一个代表恒定电抗。恒定电阻线在X轴附近对称。电抗在开路附近时，阻抗等于并联电阻。由于电抗降低，曲线路径沿圆圈至起点，其在电感分量时为正，而在电容分量时为负。由于电抗降低，曲线趋向于零。在1/2并联电阻距离处，圆以X轴为中心，其半径相同。

        另外，需要注意的是，起点和圆上某点的连线的斜率便为该电路的Q。这就是说，最低Q出现时并联电抗的值更大，而最高Q出现时并联电抗较低。关于该圆的另一件有趣的事情是，它可以表明并联谐振L-C-R电路的阻抗。参考恒定并联R曲线，在低频率下，电感阻抗较小，而您开始于起点。随着频率上升，阻抗在首个四分之一圆内为正，直到电容电抗等于谐振电感反应（X轴上的1）。之后，您转入第二个四分之一圆，并绕圆继续。

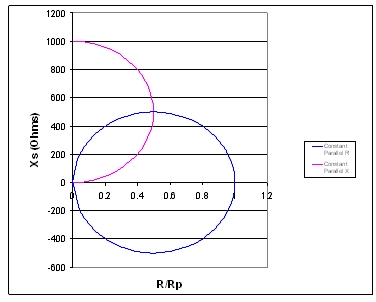
　　图2：恒定并联电阻映射为一个圆。

       第二条曲线表明固定电抗和并联可变电阻的阻抗圆。它具有同恒定不变R曲线相同的形状，但其以Y轴为中心。

       那么该如何使用它呢？在您需要估算电感DC电阻（DCR）和电容等效串联电阻（ESR）对电源滤波器输出阻抗影响程度时，其将会很有用处。图3对此进行了说明。输出阻抗在谐振时达到最高，因此必须首先计算出滤波器谐振频率。下一步，对电感-DCR组合和电容-ESR组合进行串-并联转换。最后，简单地组合三个已为并联的并联电阻。例如，如果您有了一个基本为0 Ohm ESR的47uF陶瓷电容，以及一个50 mOhm DCR的10μH输出电感。谐振频率为7kHz。这一频率下，电感有0.4 Ohm的电抗，从而得到Q为8，而并联电阻为3 Ohm。一种更快速的方法是将特性阻抗（（L/C）0.5）用于谐振下的电感电抗。

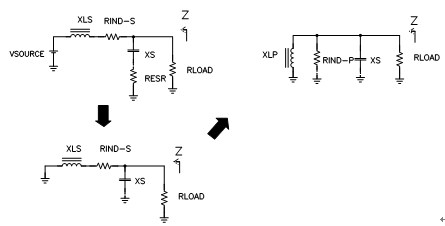
　　图3：串-并联转换简化了电路分析。

　　如欲了解本文章内容及其他电源解决方案的更多详情，敬请访问：www.ti.com.cn/power。

　　附录1：并联电路的串联转换。

　　在某个频率下，图1所示的两个电路等效。计算并联部分的串联等效电路：

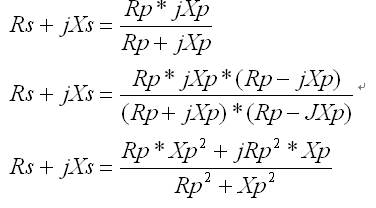
　　让实数和虚数项相等，分子和分母均除以Xp2，代入Q=Rp/Xp。

　　类似地，求解Xs。

　　作者：Robert Kollman

　　德州仪器（TI）