3相3级逆变器的中心对齐SVPWM实现

3 主扇区计算简单方法
利用α- β坐标平面Vref角度，可计算出该主扇区。如图2和图3所示，每个主扇区均位于固定角度范围内。例如，第一个主扇区的角度范围为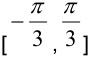 。还可以计算第二个主扇区的角度范围，其为 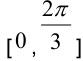。因此，第一个和第二个主扇区之间的重叠区域，会延伸到两个相邻区域。这些重叠区域增加了主扇区的计算难度。为了规定每个扇区的独占角度区域，我们可重新定义主扇区，如图6所示。

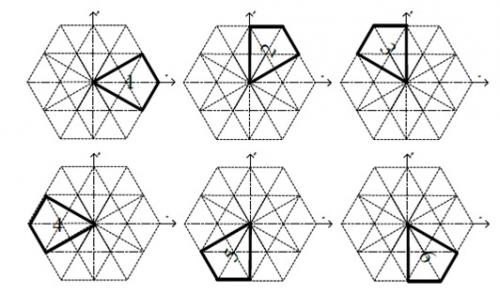
图6 主扇区新定义

利用图6所示定义，每个主扇区都有其自己的角度区域及其自己的子扇区。

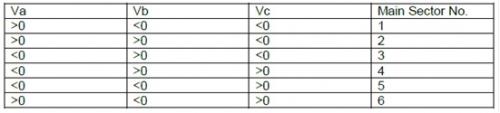
鉴于图7所示3相电压波形，相应主扇区被标记在正确位置。由图7，表3总结了主扇区编号与3个相位元素之间的关系，其可帮助轻松确定主扇区。

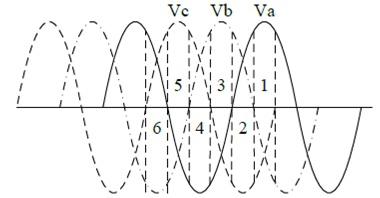
图7 主扇区位置

表3 主扇区确定方法

4 子扇区过程
在2级SVPWM中，第1步是找出可确定停顿矢量的扇区编号。第2步是，计算每个所选矢量的停顿时间。根据第1章中3级SVPWM原则，当确定主扇区且所有矢量均映射到主扇区时，可使用与2级SVPWM相同的过程来确定子扇区，并计算每个停顿矢量的停顿时间。这种过程算法在许多文章中都有介绍，因此本文将不再讨论子扇区确定方法和停顿时间计算方法。

尽管我们可以通过子扇区方法找出每个矢量的停顿时间，但是每个功率开关的占空比分布比2级SVPWM要复杂得多。3级SVPWM拥有6对补偿功率开关，其意味着，当我们得到所选矢量的停顿时间时，必须计算出6个占空值。为了简化占空比计算过程，本文介绍一种有效的方法，用于轻松地计算每对功率开关的占空比。

我们同样以主扇区1作为例子。根据图4，R相位没有N状态。除此以外，如果选择OON、ONO和OOO，用于矢量映射，则S和T相位没有P状态。就R相位而言，用1代替P状态，并用0代替O状态。就S和T相位而言，用1代替O状态，用0代替N状态。结果是，与2级SVPWM相同的矢量图。图8显示了这种操作过程。

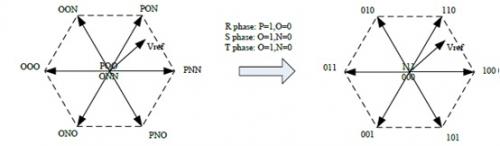
图8 状态代替

在完成2级SVPWM过程以后，可知道3个矢量的停顿。如图8所示，Tx为100停顿时间，Ty为110停顿时间，而Tz为111和000停顿时间。因此，我们可以利用中心对齐PWM输出模式，计算出3对补偿功率开关的3个占空比（d1、d2和d3）；本例所得矢量序列为000→100→110→111→110→100→000。图9左边显示了2级SVPWM中3对补偿功率开关上级开关的状态，其被称作中心对齐SVPWM。

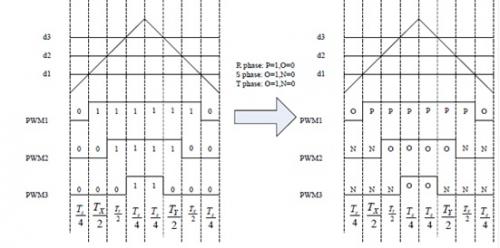
图9 2级逆变器中心对齐SVPWM

如果我们用P和N分别代替1和0，则我们可得到3级逆变器中心对齐SVPWM的右边部分。3级SVPWM的矢量序列为：

ONN→PNN→PON→POO→PON→PNN→ONN。

正功率开关对为Qx1和Qx3（x=R、S、T）；负功率开关对为Qx4和Qx2（x = R、S、T）。我们对每对状态0和1的定义也与2级SVPWM相同。因此，对于主扇区1而言，在单开关周期内，负R相位对始终为0，对于S、T相位而言，正对始终为0。那么，仅3对功率开关必须通过不同的占空比、正R相位对和负S、T相位对控制，其相当于2级SVPWM的3对功率开关。这意味着，在主扇区1中，d1可分配给正R相位对，d2可分配给负S相位对，而d3可分配给负T相位对。

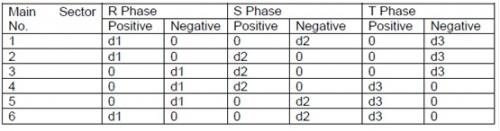
前面分析结果可扩展至其它矢量。表4总结了状态代替，表5列举了每个主扇区的占空比分配情况。

表4 每个主扇区的状态代替

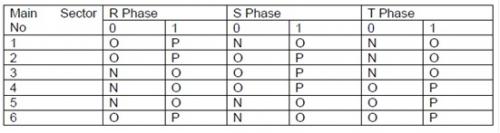
表5 每个主扇区的占空比分配

5 算法实施
由第4小节的分析，我们可实现3级SVPWM算法。图10显示了该软件流程图。

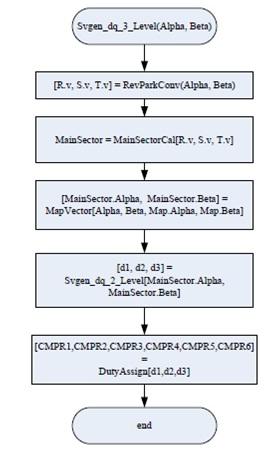
图10 3级SVPWM算法流程图

图10中，所有函数输入均为基准矢量的αβ元素。

RevParkConv为Park反向转换的函数，由此，我们可以得到3个相位静态元素。
MainSectorCal为通过表3所列结果确定主扇区编号的函数。

MapVector为映射基准矢量至所选主扇区的函数。表2列出了映射矢量αβ元素。
Svgen_dq_2_Level为实现2级SVPWM过程的函数，由此，我们可知道三个占空比d1、d2和d3。

DutyAssign为通过表5所列结果为功率开关对分配CMPR值的函数。

6 仿真结果
为了测试第5章所讨论算法的有效性，我们使用Matlab Simulink Platform得到仿真结果。所有算法均通过C代码s函数完成，其可轻松移植至现实系统。

仿真条件如下：
三相三级NPC桥
开关频率：10kHz、PWM周期计数：3000
DC侧电压：700V
基准相到相电压：（1）200 V/50 Hz；（2）280 V/50 Hz
LC滤波器参数：每个相位，L=9mH，C=4.7μf
R负载：每个相位100Ω
无停滞时间

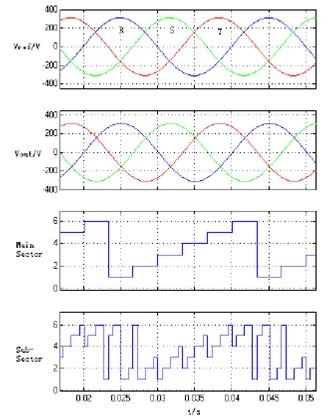
图11仿真结果

（CH1：基准电压；CH2：输出电压；CH3：主扇区计算；CH4：子扇区计算）

图12 仿真结果