基于自谐振频率电容器种类的选择算法

（1）确定VRM不再能提供低阻抗时的频率点，作为设计频段的起点FLF.代码实现为：

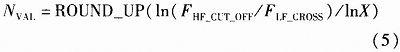
（2）确定设计频段的最高频率点，即截止频率FHF.（3）将设计频段在对数坐标下平均划分为N段，N依赖于电容器最大种类数。代码实现为：

（4）获得每种电容器的自谐振频率。代码实现为：FselfO=[Fb1；Fb3；Fb4；Fb5；Fb6；Fb7；F1；F2；F3；F4；F5；F6；F7；F8；F9；F10；F11；F12]；％从小到大排列电容器的自谐振频率。

（5）根据电容器的自谐振频率，从1～N段，依次寻找自谐振频率落在该段的电容器。显然，电容器的自谐振频率均位于频段中点最理想。但更多情况下，只能挑选一个离频段中点最接近的电容器。为避免重复选择一种电容器，每次都会判断该电容器是否已经被选择，如果被选择过，则继续在其他电容器中寻找。

这种算法在本质上与Flat Response与Decade Methods相同，同样要保证所选电容器能尽量覆盖整个需要设计的频段，从而达到在每个频率点都有提供低阻抗电容器的目的。这样，无论并联谐振峰值在哪个频率点，都不会出现设计漏洞，保证了设计的可靠性。

相对于Flat Response与Decade Methods，这种算法的优点在于：

（1）限制条件比较少，更适合于实际中PDN网络的设计。

（2）不需要知道过多与电容器相关的具体参数，仅需提供与其相对应的自谐振频率即可，将设计者从繁琐的ESL、ESR和C的限制中解脱出来。

（3）将容值的选择问题直接转化为自谐振频率的选择问题，从而将PDN网络设计彻底搬进频域，更加直观和易于理解。

经过反复验证，该算法在容值种类为4种及以上时，可以得到最佳方案。

但这种算法对于只可使用一种电容器的情况并不适用。通过实验发现，当仅使用一种电容器时，该电容器的容值与截止频率、目标阻抗以及并联谐振峰值均有较大关系。也就是说，无论将电容器的自谐振频率选择在并联谐振峰值处，还是在对数坐标中设计频段的中点，或选用所提供的最大容值的电容器，都不能保证是电容器数目最小的方案。鉴于仅用一种电容器时，其数目的计算仅是简单地增加电容器的数量直到满足条件为止，文中采用尝试比较的方法，以设计频段的中点为中心，取其周围4种电容器分别进行设计，选出使用个数最少的电容器作为最终方案。

当可使用两种电容器时，文中所提算法选择出的两个电容器的自谐振频率分别在FLF和截止频率。通过验证，这种选取并不是最佳方案。这里进行了几种方案的尝试：

（1）在设计频段的中间选择两个电容器。

（2）在FLF和并联谐振频率各选择一个电容器。

（3）在并联谐振频率和截止频率各选择一个电容器。

通过比较，第2种方案需要的电容器个数最少。所以，文中默认在FLF和并联谐振频率各选择一个电容器是最佳方案。该方案代码实现为：

对于选择3种电容器的情况，文中算法的性能依赖于所选的截止频率。如果截止频率较高，该算法依然能得到较好的方案，但截止频率较低时，结果并不理想，必须寻找更加稳定的算法。

这里进行了几种方案的尝试：

（1）在设计频段的中间选择3个电容器。

（2）在FLF截止频率以及并联谐振频率处各选择一个电容器。

通过比较，第2种方案使用的电容器个数最少，即最件方案。

显然，当两个电容器的自谐振频率差距很大时，应让第3个电容器的自谐振频率和并联谐振频率一致。

以下案例的目标阻抗为0．01 Ω，截止频率为20 MHz，对比分别由3种算法得出的PDN阻抗曲线如图2～图4所示。

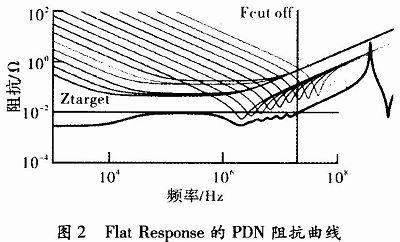
从以上图中可以看出，在使用电容器数目基本一致的情况下，文中算法与Flat Response和Decade Methods的效果一样好，但文中算法要求更易于实现，更设和应用于工程设计。

3 结束语

通过介绍经典的去耦电容器的选择算法，引出了文中提出的基于自谐振频率的电容器选择算法，阐述了文中算法相对于经典算法的优势，通过此算法已经成功运用于PDN前仿真工具中，效果理想。