精密SAR模数转换器的前端放大器和RC滤波器设计

逐次逼近型（SAR）ADC提供高分辨率、出色的精度和低功耗特性。一旦选定一款精密SARADC，系统设计师就必须确定获得最佳结果所需的支持电路。需要考虑的三个主要方面是：模拟输入信号与ADC接口的前端、基准电压源和数字接口。本文将重点介绍前端设计的电路要求和权衡因素。关于其它方面的有用信息，包括具体器件和系统信息，请参阅数据手册和本文的参考文献。

前端包括两个部分：驱动放大器和RC滤波器。放大器调节输入信号，同时充当信号源与ADC输入端之间的低阻抗缓冲器。RC滤波器限制到达ADC输入端的带外噪声，帮助衰减ADC输入端中开关电容的反冲影响。

为SARADC选择合适的放大器和RC滤波器可能很困难，特别是当应用不同于ADC数据手册的常规用途时。根据各种影响放大器和RC选择的应用因素，我们提供了设计指南，可实现最佳解决方案。主要考虑因素包括：输入频率、吞吐速率和输入复用。

选择合适的RC滤波器

要选择合适的RC滤波器，必须计算单通道或多路复用应用的RC带宽，然后选择R和C的值。

图1显示了一个典型的放大器、单极点RC滤波器和ADC.ADC输入构成驱动电路的开关电容负载。其10MHz输入带宽意味着需要在宽带宽内保证低噪声以获得良好的信噪比（SNR）。RC网络限制输入信号的带宽，并降低放大器和上游电路馈入ADC的噪声量。不过，带宽限制过多会延长建立时间并使输入信号失真。

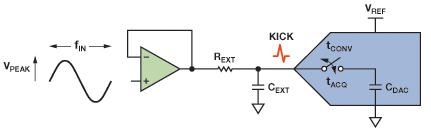
图1.典型放大器、RC滤波器和ADC

在建立ADC输入和通过优化带宽限制噪声时所需的最小RC值，可以由假设通过指数方式建立阶跃输入来计算。要计算阶跃大小，需要知道输入信号频率、幅度和ADC转换时间。转换时间tCONV（图2）是指容性DAC从输入端断开并执行位判断以产生数字代码所需的时间。转换时间结束时，保存前一样本电荷的容性DAC切换回输入端。此阶跃变化代表输入信号在这段时间的变化量。此阶跃建立所需的时间称为"反向建立时间"。

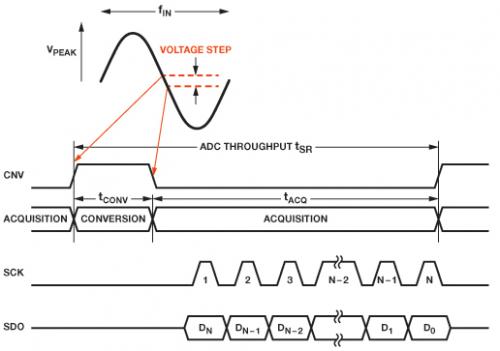
图2.N位ADC的典型时序图

在给定输入频率下，一个正弦波信号的最大不失真变化率可通过下式计算：

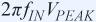
如果ADC的转换速率大大超出最大输入频率，则转换期间输入电压的最大变化量为：

这是容性DAC切换回采集模式时出现的最大电压阶跃。然后，DAC电容与外部电容的并联组合会衰减此阶跃。因此，外部电容必须相对较大，达到几nF。此分析假设输入开关导通电阻的影响可忽略不计。现在需要建立的阶跃大小为：

接下来计算在ADC采集阶段，ADC输入建立至½LSB的时间常数。假设阶跃输入以指数方式建立，则所需RC时间常数τ为：

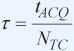
其中，t_ACQ为采集时间，N_TC为建立所需的时间常数数目。所需的时间常数数目可以通过计算阶跃大小V_STEP,与建立误差（本例为½LSB）之比的自然对数来获得：

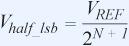
因此，

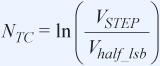
将上式代入前面的公式可得：

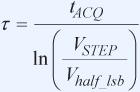
等效RC带宽=

示例：借助RC带宽计算公式，选择16位ADCAD7980（如图3所示），其转换时间为710ns，吞吐速率为1MSPS，采用5V基准电压。最大目标输入频率为100kHz。计算此频率时的最大阶跃：

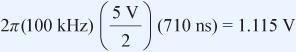
然后，外部电容的电荷会衰减此阶跃。使用27pF的DAC电容并假设外部电容为2.7nF，则衰减系数约为101。将这些值代入V_STEP计算公式：

接下来计算建立至½LSB（16位、5V基准电压）的时间常数数目：

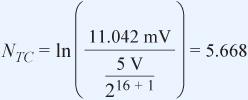
采集时间为：

计算τ：

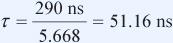
因此，带宽为3.11MHz，R_EXT为18.9?。

图3.采用16位1MSPSADCAD7980的RC滤波器

最小带宽、吞吐速率和输入频率之间的这种关系说明：输入频率越高，则要求RC带宽越高。同样，吞吐速率越高，则采集时间越短，从而提高RC带宽。采集时间对所需带宽的影响最大；如果采集时间加倍（降低吞吐速率），所需带宽将减半。此简化分析未包括二阶电荷反冲效应，它在低频时变成主要影响因素。输入频率非常低时（<10kHz，包括DC），容性DAC上建立的始终是大约100mV的电压阶跃。此数值应作为上述分析的最小电压阶跃。

多路复用输入信号很少是连续的，通常由不同通道切换产生的大阶跃组成。最差情况下，一个通道处于负满量程，而下一个通道则处于正满量程（见图4）。这种情况下，当多路复用器切换通道时，阶跃大小将是ADC的满量程，对于上例而言是5V。

图4.多路复用设置

在上例中使用多路复用输入时，线性响应所需的滤波器带宽将提高到3.93MHz（此时阶跃大小为5V，而非单通道时的1.115V）。假设条件如下：多路复用器在转换开始后不久即切换（图5），放大器和RC正向建立时间足以使输入电容在采集开始前稳定下来。

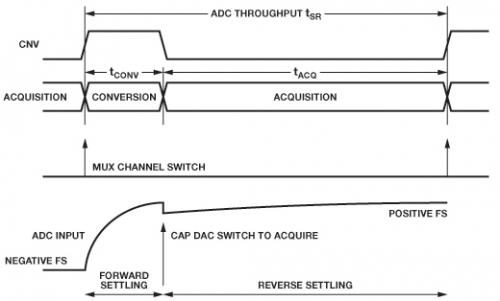
图5.多路复用时序

对于计算得到的RC带宽，可以利用表1进行检查。从表中可