放大器建模为模拟滤波器可提高SPICE仿真速度

设置 C₁ = 10 nF，然后选择C₂ ，使得根号下的量为正数。为方便起见，选择C₂ 为 10 pF。代入已知值 C₂ = 10 pF、 a₁ = 3.67E6、K = 5、 a₀ = 17.86E12 ，计算R₂值：

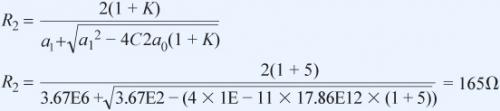
R₁ 的值很容易计算，等于 R₂/K = R₂/5 = 33。根据标准多项式系数可求解 R₃。代入a₀、R₂和 C₂ 的已知值可得：

最后，验证元件比是否正确，即代入a₀、R₂、 R₃、增益K和 C₂ (从s 项求得)的已知值时，C₁ 应等于10 nF。

得出元件值后，再代入方程式中，验证多项式系数在数学上是否正确。利用电子表格计算器就能轻松完成这项工作。所示的元件值是可以用于最终SPICE模型的实际值。实际应用中，应确保最小电容值不低于10 pF。

5倍增益放大器的网络列表如下文所示，模型则如图8所示。G1是开环增益为120 dB的VCCS（压控电流源）。注意，如果使用电阻、电容、二极管和非独立源，所需的元件数将多得多。

.SUBCKT MFB +IN –IN OUT

***VCCS – 120 dB OPEN_LOOP_GAIN***

G1 0 7 0 6 1E6

R1 4 3 330

R3 6 4 34K

C2 7 6 1P

C1 0 4 1N

R2 7 4 1.65K

E2 3 0 +IN –IN 1

E1 9 0 7 0 –1

***OUTPUT_IMPEDANCE RO = 2 Ω***

RO OUT 9 2

.END

图8. 采用MFB滤波器的5倍增益放大器仿真电路

设计示例：10倍增益放大器
在第二个示例中，考虑一个无过冲10倍增益放大器的脉冲响应，如图9所示。建立时间约为7 μs。由于无过冲，脉冲响应可以近似为具有临界阻尼， ζ ≈ 0.935 (M_p = 0.025%)。

图9. 无过冲10倍增益放大器

在无过冲的情况下，很容易保持恒定的建立时间，并调整阻尼比以模拟正确的带宽和峰化。图10显示了极点如何随阻尼比而变化，与此同时建立时间保持不变。图11显示了频率响应的变化情况。

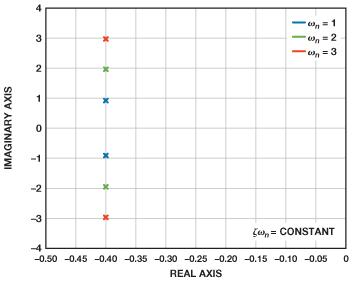
图10. 不同阻尼比对应的极点位置，建立时间保持不变

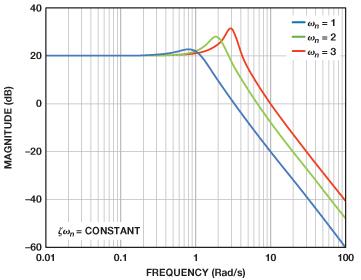
图11. 不同阻尼比对应的频率响应，建立时间保持不变

***AD8208 PREAMPLIFIER_TRANSFER_FUNCTION (GAIN = 20 dB)***

.SUBCKT PREAMPLIFIER_GAIN_10 +IN –IN OUT

E1 OUT 0 LAPLACE {V(+IN)–V(–IN)} = {3.734E12 / (S^2 + 1.143E6*S + 373.379E9)}

.END

为求得单位增益拓扑的电阻和电容值，请像前面一样选择R₁ = R₂ = 10 kΩ 。利用与5倍增益放大器示例相同的方法计算电容值：

网络列表如下文所示，Sallen-Key仿真电路模型则如图12所示。E2是一个10倍增益模块，与一个2 Ω输出阻抗一起置于输出级。E2将单位增益传递函数放大10倍。拉普拉斯变换和Sallen-Key网络列表产生的仿真相同，如图13所示。

***AD8208 PREAMPLIFIER_TRANSFER_FUNCTION (GAIN = 20 dB)***

.SUBCKT AMPLIFIER_GAIN_10_SALLEN_KEY +IN –IN OUT

R1 1 4 10E3

R2 5 1 10E3

C2 5 0 153E–12

C1 2 1 175E–12

G1 0 2 5 2 1E6

E2 4 0 +IN –IN 10

E1 3 0 2 0 1

RO OUT 3 2

.END

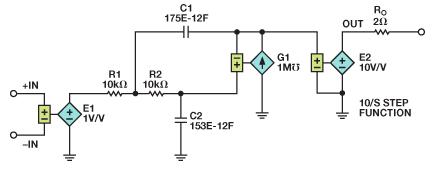
图12. 采用Sallen-Key滤波器的10倍增益放大器仿真电路

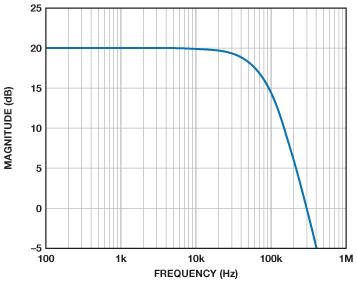
图13. 采用Sallen-Key滤波器的10倍增益放大器的频域仿真

利用MFB拓扑可以进行相似的推导。网络列表如下文所示，仿真模型则如图14所示。

***AD8208 PREAMPLIFIER_TRANSFER_FUNCTION (GAIN = 20 dB)***

.SUBCKT 8208_MFB +IN –IN OUT

***G1 = VCCS WITH 120 dB OPEN_LOOP_GAIN***

G1 0 7 0 6 1E6

R1 4 3 994.7

R2 7 4 9.95K

R3 6 4 26.93K

C1 0 4 1N

C2 7 6 10P

EIN_STAGE 3 0 +IN –IN 1

***E2 = OUTPUT BUFFER***

E2 9 0 7 0 1

***OUTPUT RESISTANCE = 2 Ω***

RO OUT 9 2

.END

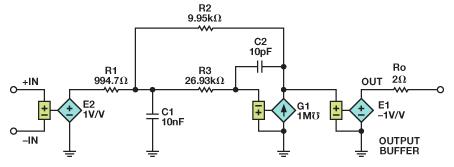
图14. 采用MFB滤波器的10倍增益放大器仿真电路

结束语
对于高带宽放大器，与利用s域（拉普拉斯变换）传递函数相比，利用模拟元件构建SPICE模型能够提供快得多的时域仿真。Sallen-Key和MFB低通滤波器拓扑提供了一种将s域传递函数转换为电阻、电容和压控电流源的方法。

MFB拓扑的非理想操作来源于 C₁ 和 C₂ 在高频时表现为相对于电阻R₁、 R₂和R₃的阻抗短路。同样，Sallen-Key拓扑的非理想操作来源于C₁ 和 C₂ 在高频时表现为相对于电阻 R₁ 和 R₂的阻抗短路。这两种拓扑的对比如图15所示。

现有常用于CMRR、PSRR、失调电压、电源电流、频谱噪声、输入/输出限幅及其它参数的电路可以与该模型合并，如图16所示。

图15. Sallen-Key和MFB拓扑的波特图

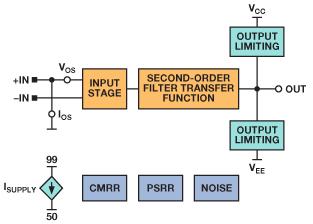
图16. 包括误差项的完整SPICE放大器模型

参考文献
Karpaty, David. "Create Spice Amplifier Models Using Second-Order Approximations." Electronic Design, September 22, 2010.

作者简介

David Karpaty [da