高频和微波功率基准及其应用研究----微量热计基本理论研究(三)

。根据功率测量公式，热敏电阻功率座入射功率P_IN计算式为

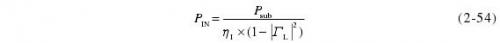
其中，η_I为微量热计定标的有效效率，Γ_L是功率座的反射系数，P_sub是P_IN在热敏电阻上的直流替代功率。而实际上输入功率P_IN应为

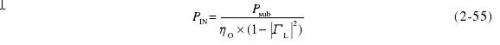
其中η_O为实际测量时的有效效率，用式（2-52）表示。

根据以上分析可知，这种情况下功率测量的热等效误差表达式为

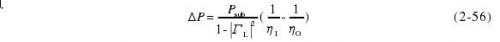
相对热等效误差表达式为

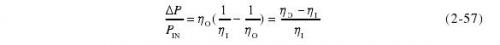
根据热敏电阻功率座校准因子的定义，式（2-57）可写作

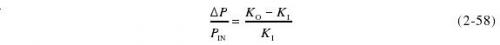
其中K_o为实际测量时的校准因子，K_I为微量热计定标得到的校准因子。式（2-58）说明，功率测量的相对热等效误差即为校准因子的相对偏差。

对采用等温方式定标的功率座，其η_I为η_S，则式（2-58）可表示为

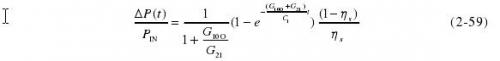
稳态表达式为

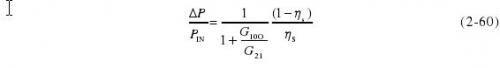
对采用升温方式定标的功率座，若其有效效率η_I已按式（2-50）修正，由于ηI近似等于效率，可认为其热等效误差的情况与等温方式相同。

若未修正，η_I表示式为（2-39），则式（2-57）可表示为

稳态表达式为

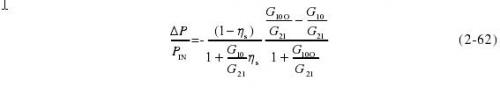
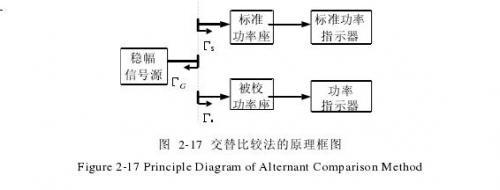
2）微量热计定标后的热敏电阻功率座用于量值传递。在第4章中将对功率量值传递进行详细的研究，在这里只就最简单的功率量值传递方法－交替比较法进行阐述，因为交替比较法是其他方法的基础，所以这里的结论对其他量值传递方法也同样适用。

图2-17是交替比较法的原理框图，因为热敏电阻功率座一般用于量值传递，已经很少用于功率测量，所以这里只考虑标准座是热敏电阻功率座而被较功率座是非热敏电阻功率座的情况。根据交替比较法的原理，可得

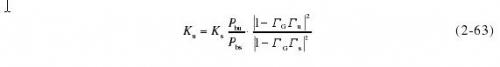
其中Ks和Ku分别是标准座和被校座的校准因子，P_bs和P_bu分别是标准座和被校座的功率指示器示数。

在Ks应为Ko而实际使用KI计算Ku时，根据式（2-63）可以推导得到Ku的相对偏差为

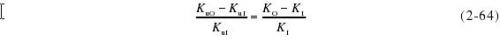
其中K_uO和K_uI分别为根据K_O和K_I计算的Ku值。由式（2-64）可见，在使用热敏电阻功率座进行量值传递时，功率测量的热等效误差也被传递了。

2.4.4热等效误差的减小

根据以上的分析可见，无论微量热计采用哪种定标方式都会带来热等效误差，误差的大小除了与热敏电阻功率座内外的热导有关，与其效率有关外，还与测量时间有关，所以无法对这项误差进行补偿，只能在微量热计定标和功率两个环节采取措施，使在微量热计中的有效效率定标值和功率测量中的有效效率尽可能接近效率，以减小热等效误差对功率测量的影响。

通过对微量热计中有效效率的分析可知，对升温方式的微量热计来说，为了减小有效效率和效率的偏差，应根据式（2-50）对有效效率测量结果进行修正。如上一节所述，η_effC与效率的差为

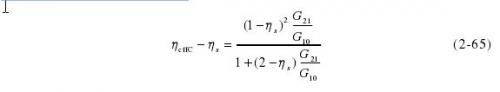
尽管对有效效率的修正能有效的减小其与效率的偏差，但当G21/G10较大时，修正的作用有限。例如当效率ηs =0.9，G21/G10 =1时，修正后的偏差约为0.5%.图2-18给出了不同条件下，升温方式修正后的有效效率与效率偏差曲线。

从图2-18可以看出，应对用于升温方式微量热计的热敏电阻功率座特性有严格的要求，效率不应低于85%，G21/G10不应大于0.1，否则的话，相对于等温方式和量热计方式功率基准的偏差过大，不利于世界功率量值的统一。这也是NIST在国际比对后急于重新设计和加工其热敏电阻功率座的原因。

对于采用等温方式的微量热计来说，定标得到的有效效率值就是效率，无须改进和修正。加拿大的波导功率基准和第3章将介绍的我国宽带同轴功率基准均采用等温方式，国际比对结果证明了等温方式得到的有效效率和修正后的升温方式得到的有效效率的一致性。