如何处理高di/dt负载瞬态(下)

在《如何处理高di/dt负载瞬态（上）》中，我们讨论了电流快速变化时一些负载的电容旁路要求。我们发现必须让低等效串联电感（ESL）电容器靠近负载，因为不到0.5 nH便可产生不可接受的电压剧增。实际上，要达到这种低电感，要求在处理器封装中放置多个旁路电容器和多个互连针脚。本文中，我们将讨论达到电源输出实际di/dt要求所需的旁路电容大小。

为了讨论方便，图1显示了电源系统的P-SPICE模型。本图由补偿电路电源、调制器（G1）和输出电容器组成。内部还包括互连电感、旁路电容负载模型、DC负载和步进负载。

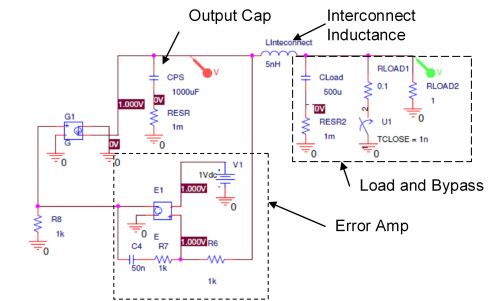
图1简易P-SPICE模型辅助系统设计

首先，你需要决定是将电源和负载看作一个个单独的"黑匣子"，还是把问题当作一个完整的电源系统设计来处理。如果使用系统级方法，你可以利用负载旁路电容来降低电源输出电容，从而节约系统成本。如果使用"黑匣子"方法，你要单独测试电源和负载。不管使用哪种方法，你都要知道负载需要多大的旁路电容。

首先，估计电源和负载之间的互连电感和电阻的大小。这种互连阻抗(L_INTERCONNECT) 形成一个旁路电容器 (C_BYPASS) 低通滤波器。我们假设电源输出阻抗较低。利用该低通滤波器的特性阻抗 (Z_O)、负载步进值 (I_STEP) 和允许电压波动（dV），建立旁路滤波器要求（方程式1-2）：

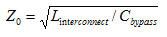方程式 1

方程式 2

求解方程式2得到Z₀，然后代入方程式1，得到方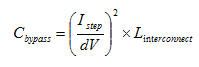程式3：

方程式 3

有趣的是，所需电容大小与负载电流的平方除以允许扰动的平方有关，因此要仔细计算这两个值。

互连电感的范围从并列电源的几十nH，到远距放置电源的数百nHs。一条较为有效的经验法则是，每英寸增加15 nH左右的互连电感。负载步进为10安培且允许扰动为30mV时，旁路要求范围为5 nH的500 uF到500 nH的50 mF。

另外，这种滤波器还降低了电源的负载电流上升速率。如果无损滤波器由一个电流方波激励，则电感电流为正弦。通过对方程式4-7中的电流波形求微分，可以计算得到上升速率。

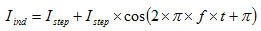方程式 4

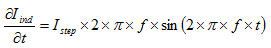方程式5

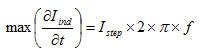方程式6

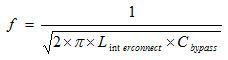方程式7

互连电感为5 nH，旁路电容为500 uF时，10安培步进变化可形成0.2 A/uS电源电流上升速率。更大的电感可产生更低的di/dt。这些数值比系统设计人员所规定的值要小得多。

使用系统级方法时，要在最大化环路带宽的同时，最小化总电容。现在，请您思考如何使用"黑匣子"方法。你必须在没有旁路电容和最大期望旁路电容的情况下，让电源稳定。如前所述，互连电容会推高负载的旁路电容要求。使用"黑匣子"方法时，这反过来又会影响电源的电容。连接电容范围确定了电源的交叉频率范围。在电压和电流两种模式下，两者均成比例关系。你可以最大化无负载电容的交叉频率，但只要连接负载，交叉频率就会急剧下降。

表1对举例系统三个互连电感的要求电容器进行了比较。通过改变互连电感、计算负载旁路电容并设计电源的相应输出级和控制环路，得到比较数据。案例1的负载和电源并列放置；案例2电源和负载之间的互连电感大小为中等。案例3中，使用线缆连接的电源的电感极高。要求旁路的多少直接与互连电感有关。

本例中，案例 3 是互连电感的 100 倍，旁路电容也是如此。这在电源设计中形成纹波，原因是电源在有和没有旁路电容器的情况下都必须保持稳定。很明显，第一种方法更好，因为它使用的电容器最少，成本最低。案例2中，互连电感受到一定的控制，电容器数量有一定增加。案例3中，大量的互连电感带来了严重的成本问题。案例2和案例3也都有一个好处：独立的电源测试。

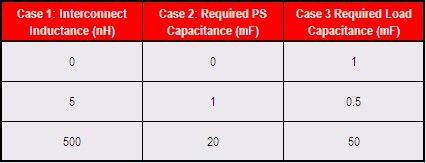
表1利用系统级方法降低电源系统成本

图 2 对小和大互连电感的负载瞬态期间的输出电压变化模拟情况进行了比较。小电感响应快速渐次减弱，而大电感则并非如此，花费了较长的时间才稳定下来。这是由于特性阻抗更高以及谐振频率更低。另外，如果负载电流在该谐振频率有规律地跳动，则会出现极宽且具破坏性的电压变化。

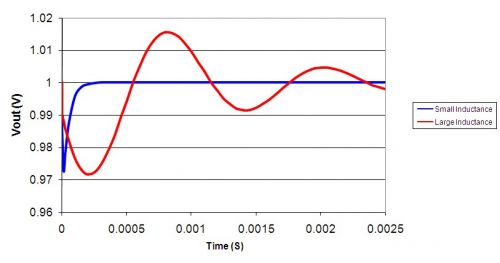
图 2 电压振铃成为大互连电感的一个问题

总之，高di/dt负载要求小心谨慎地进行旁路设计，以保持电源动态调节能力。在负载和旁路电容器以及旁路电容器和负载之间，必须使用低电感互连。系统级方法可实现一种成本最低的解决方案。为了系统测试方便，许多系统工程师都忽略了这种通过降低电源电容实现成本节省的解决方案。

以后，我们将对一些根据经验所得的结论进行讨论，以确定同步降压结构的最佳栅极驱动计时方案，敬请期待。

如欲了解有关本解决方案及其他电源解决方案的更多详情，敬请访问官方网站。

深入阅读：如何处理高di/dt负载瞬态