移相全桥ZVS DC/DC变换器的极点配置自适应预测控制

稳定度。控制方法是用状态变量IL和Uc同参考值比较所得的误差乘以反馈矩阵－l得到占空比的扰动值,即

D′=－lx l=〔l1－l2〕（6）

　　将式（6）代入式（2）得

x(k＋1)=(A－lB)x(k)（7）

　　从而系统得特征方程为

det[ZI－A＋lB]=0（8）

　　假设我们根据电源的动态要求，获得了所希望的极点为a1和a2，则系统希望的特征方程为

Z2－(a1＋a2)Z＋a1a2=0（9）

　　通过对比式（8）和式（9），状态反馈矩阵l很容易求出，这样就可以把极点配置到指定点上。但是，由于矩阵B是输入电压Vin的函数，相应的反馈矩阵系数l也是输入电压的函数，它会随着输入电压的变化而变化。因此，需要不断地根据输入电压的变化来调整反馈矩阵系数l，以满足要求的动态响应，这样就实现了自适应控制，从而提高了整个控制系统的控制性能。

4 控制算法的方框图及算法流程图

　　图4是用DSP实现移相全桥变换器数字控制的方框图。DSP的主要作用是根据输入电压，输出电感电流预测值IL′和输出电容电压预测值Vc′计算出变换器的占空比D，使全桥变换器的输出电压稳定在所要求的输出电压值。其计算方程式为

D=Dop＋[－l1 －l2]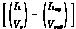（10）

　　式（10）概括了本文所提出的基本控制思想。由于上述预测估算是每2个采样周期更新一次控制量，因此占空比也是每2个周期更新一次。

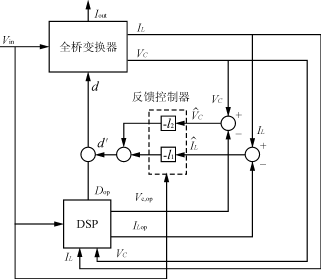
图4 控制系统方框图

　　驱动信号算法流程图如图5所示,从这里可看出根据准线性模型算出的占空比Dop是变化的，它决定了移相全桥变换器工作点的变化轨迹，且控制算法能根据变换器的动态变化不断调整系统的反馈矩阵系数l，以达到控制系统所要求的动态响应。

图5 算法流程图

　　5 Matlab仿真结果

　　设定移相全桥变换器的各项仿真参数如下：

　　变压器副边与原边的匝数比n=1∶3；谐振电感L1=17μH；滤波电容C=470μF；滤波电感L=360μH；开关频率fs=100kHz；Rd=4n2LRFs；开关周期Ts=10μs；输出电压为U=50V。在这里设置希望配置的极点(Z域)为0.4＋0.5j和0.4－0.5j,但它不一定是最优化的极点。

　　为了测试这种控制策略的有效性，进行以下仿真。

　　1）在设定初始占空比D=0.28时，系统从初始

　　零状态到稳态时的输出电压仿真波形，如图6所示。

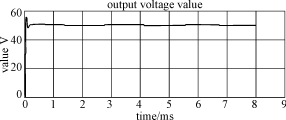
图6 初始状态到稳态过程的输出电压仿真波形

　　从图6中可以看出控制系统经过大约200μs就能达到稳定，超调量为6V，控制系统得动态响应较快。

　　2）当输入电压由220V突变为180V时，输出电压变化的仿真波形，如图7所示。从图7中可以看出，控制系统在输入电压突变时，从一个稳定状态调整到另一个稳定状态需要大约3ms，输出电压的波动很小，最大为0.12V。

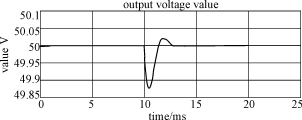
图7 输入电压突变时输出电压变化过程的仿真波形

　　3）当负载由5Ω突变为10Ω时，输出电压变化的仿真波形，如图8所示。从图8中同样可以看出，控制系统在输出负载突变时，从一个稳定状态调整到另一个稳定状态需要大约3ms，且输出电压的波动很小,大约为0.2V。

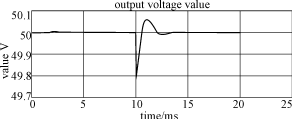
图8 负载突变时输出电压变化过程的仿真波形

　　从以上仿真波形可以看出，使用以上控制算法可使移相全桥变换器有较好的动态响应和稳定性,并且控制算法简单，易于实现。

　　6 结语

　　本文介绍了移相全桥变换器采用准线性建模和极点配置自适应数字控制的控制思想。准线性模型可以很好地描述系统在大扰动下的工作特性，极点配置自适应数字控制综合了自适应控制和极点配置控制两者的优点，通过仿真证明了这种控制策略不但算法简单，实现容易，并且可以保证变换器在各稳定工作点都有很好的动态特性和稳定性。另外这种控制策略可以用TI公司的DSP作为主控芯片来实现其数字控制，使得控制系统有更高的稳定性、可靠性和更强的灵活性。