电压波动和闪变的检测与控制方法

　 0 引言

　　随着大量的基于计算机系统的控制设备和自动化程度很高的用电设备相继投入使用，工业用户对电能质量的要求越来越高，甚至几分之一秒的不正常就可造成的巨大的损失。据统计，自动化程度很高的工业用户一般每年要遭受10～50次与电能质量问题有关的干扰，其中因包括电压波动和闪变在内的动态电压质量问题造成的事故数约占事故总数的83％[1]。电压波动和闪变已成为威胁许多重要用户供电可靠性的主要原因之一，必须对其进行有效地监视与抑制。

　　电力系统的电压波动和闪变主要是由具有冲击性功率的负荷引起的[2]，如变频调速装置、炼钢电弧炉、电气化铁路和轧钢机等。这些非线性、不平衡冲击性负荷在生产过程中有功和无功功率随机地或周期性地大幅度变动，当其波动电流流过供电线路阻抗时产生变动的压降，导致同一电网上其它用户电压以相同的频率波动。这种电压幅值在一定范围内(通常为额定值的90％～110％)有规律或随即地变化，即称为电压波动。电压波动通常会引起许多电工设备不能正常工作，如影响电视画面质量、使电动机转速脉动、使电子仪器工作失常、使白炽灯光发生闪烁等等。由于一般用电设备对电压波动的敏感度远低于白炽灯，为此，选择人对白炽灯照度波动的主观视感，即"闪变"，作为衡量电压波动危害程度的评价指标。

　　1 电压波动与闪变的检测

　　1.1 调幅波检测

　　要对电压波动与闪变进行有效的抑制，首先的任务就是要准确的提取出波动信号，通常将波动电压看成以工频额定电压为载波、其电压的幅值受频率范围在0.05~35Hz的电压波动分量调制的调幅波。因此，电压波动分量的检出方法可采用通信理论中大功率载波调制信号解调方法，用与载波信号同频同相的周期信号乘以被调信号，将电压波动分量与工频载波电压分离，通过带通滤波器得到波动分量。

　　考虑电压波动分量，就是在基波电压上叠加有一系列的调幅波，为使分析简化又不失一般性，研究电压波动的检测方法可分析某单一频率的调幅波对工频载波的调制，将工频电压u(t)的瞬时值解析式写成：

　　式中：A为工频载波电压的幅值，ω0为工频载波电压的角频率，m为调幅波电压的幅值，mcos(Ωt)为波动电压。

　　目前，常用的波动电压检出方法有三种：平方解调检波法、全波整流检波法和半波有效值检波法，图1所示分别为三种方法的原理结构框图。

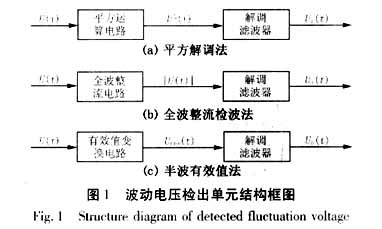
　　(1)平方解调检波法

　　国际电工委员会(IEC)推荐平方解调检测法，即将u(t)平方，然后利用解调带通滤波器检测出调幅波。经过0.05～30HZ的带通滤波器便能滤去直流分量和二倍工频分量，从而检测出mA2cos(Ωt)的调幅波即电压波动分量。这种方法较适合用数字信号处理的方法来实现。

　　(2)全波整流解调检波法

　　全波整流检波法的基本原理是将输入交流电压u(t)全波整流即进行绝对值运算后再经过解调带通滤波器后便取得波动信号。设u(t)经整流后的电压为g(t)，则g(t)可看作u(t)和幅值为±1、频率为工频的方波的乘积。将经过0.05～30HZ的带通滤波器便可检测出的调幅波即电压波动分量。

　　这种方法较适合于模拟电路加以实现，英国ERA和法国EDF等闪变仪采用此方案。它跟平方检波法一样，都要通过带通滤波器保留调幅波，但存在检出误差，误差的大小取决于波动信号的频谱结构。

　　(3)半波有效值检波法

　　半波有效值法是利用RMS/DC变换器将波动的输入交流电压变换成脉动的直流电压，再经解调带通滤波器后获得波动信号。RMS/DC变换器输出的直流电压值为输入交流电压的方均根值，其脉动成份即反映了输入电压方均根值的变化。根据半波

　　这种方法，就实际线路而言，要将方均根值的计算时间准确地整定在半个工频周期是相当困难的，而且其元件参数整定较为困难。另外，该方法可去除直流分量和二倍工频分量等，只保留调幅波，但其中不会完全没有直流分量，仍需隔直和滤波。瑞士的MEFP型闪变仪，国产的VFF-1型电压波动闪变分析仪和日本的△V10测量仪等均采用每个周波求一个有效值。

　　(4)小波多分辨率信号分解同步检波法及其它方法

　　近年来一些新理论和新原理应用于调幅波检测。如，文献[3]提出了一种采用小波多分辨率信号分解和同步检波的电压闪变信号检测新方法，该方法用小波多分辨率信号分解滤波器取代同步检波器中的解调带通滤波器，可以检测出电压闪变信号的突变时间，包络信号中的各个频率分量及其幅度。但这种方法具有对信号所需采样数据多，运算量大，检测突变故障信号的故障时刻延时较大等特点，因而在采用小波多分辨率信号分解时，必须寻求快速小波函数及其相应小波变换。

另外，文献[4]提出了一种基于随机理论